Algebra "Magic" | ||
| ||
Introduction | ||
In this section, you will learn about algebraic expressions and how to simplify them. The sections within this lesson are: |
In order to learn about algebra, we can follow a simple set of instructions, like these instructions.
If we start with the number 7 (it's an Integer because it contains no decimal values), let's follow the steps above.
If we carry out this process over and over with different starting values, we would notice that the result will always be 3 greater than the number we start with. The question is, why? In order to get the answer to this question, we need to perform some algebra. The first step asks us to choose an Integer. Let this value be called 'x' because 'x' can stand for any number.
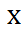 Now, we will multiply our Integer, 'x,' by two. This is the second step.
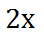 Our third step says we should add 6.
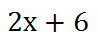 Our fourth and last step says we should divide by 2.
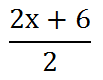 We are still left with the question, how does this result equate to being three more than the number we started with? In order to solve this dilemma, we need to factor the numerator. Notice how '2x' and '6' are both divisible by two. This means we can factor out the value two by dividing both of the terms by two.
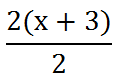 Now that we have the numerator factored, we can cancel like factors. The 2 in the numerator can be canceled with the 2 in the denominator -- by dividing the top and the bottom by two.
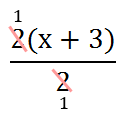 After canceling, we are left with this expression.
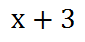 Clearly, this informs us that no matter which Integer we choose at the start, the result will always be three greater. This algebraic process proves our pattern is indeed correct. The quizmaster below is a very basic interactive problem. Use it to develop a pattern and then prove your pattern is correct using algebra.
| |
Let's take a look at a more complicated set of instructions.
If we start with a number like 12, let's follow the steps above.
If we carry out this process over and over with different starting values, we would notice that the result will always be our starting number. The question is, why do these steps give us our starting number? In order to get the answer to this question, we need to use algebra. The first step asks us to choose an Integer. Let this value be called 'x' because 'x' can stand for any number.
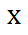 Now, we will multiply our Integer, 'x,' by 10. This is the second step.
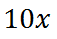 Our third step says we should divide by 2.
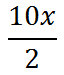 We can divide the 10 by 2 to get 5. Here is the result.
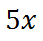 The next step is to add 5.
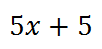 The fifth step involves dividing by 5.
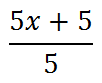 Before we proceed with the next step, look at the numerator. We can factor out a 5.
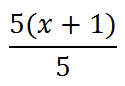 Factoring out the 5 gives us the opportunity to cancel the 5 in the numerator and the denominator -- by dividing both by 5.
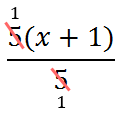 The result is a much more simplified expression, as follows.
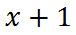 The sixth and last step has us subtracting 1.
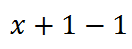 The 1 - 1 does cancel to give us this expression.
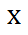 This tells us that the six step process will always give us our starting number, which is the Integer we chose in step #1.
| |
After reading the lessons, try our interactive quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
| |
Try this game, which is also about pattern recognition:
| |
Try these lessons, which are related to Algebra Magic:
| |
 uizmaster:
uizmaster:  ame:
ame:  esson:
esson: