Solving Absolute Value Inequalities | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn how to solve absolute value inequalities. Here are the topics within this page:
|
The symbol for absolute value is two vertical lines. If we were to write 'the absolute value of negative four' using symbols, it would look like this:
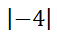
What this means relates to the definition of absolute value. The definition of absolute value for single variable problems is the distance from zero. Negative four is four units from zero, as this graphic will show.

This is how to write it symbolically.
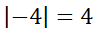
Likewise, the absolute value of 2 can be shown like this.

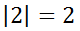
| |
To solve equations that contain absolute value symbols, let us first look at a simple equation.
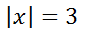
If we want to know which x-values satisfy this equation, we have to think about possible solutions. We should know there are two solutions based on this information.
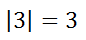
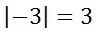
It can be seen using the number line below that 3 and -3 are both 3 units from zero.

| |
We will consider solutions to this type of absolute value equation...
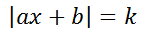
...where a, b, and k are real numbers. Since absolute value represents a distance from zero, the absolute value can never be equal to a negative value (the k-value cannot be a negative value). Distance can only be zero or greater. Therefore, if an absolute value is ever less than zero (k<0), there is no solution within the set of real numbers.
If the absolute value is equal to zero (k=0), there is only one solution within the set of real values. If the absolute value is greater than zero (k>0), there will be two solutions within the set of real values. Our next section will explore some examples.
| |
Here is our first example.
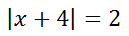
As we saw with our example from the previous section [INSERT LINK HERE], we need to form two equations when dismantling the absolute value equation. We set two equations: one with a positive right side and the other with a negative right side. This is called 'bifurcating' the absolute value equation: meaning to form two equations.
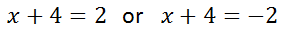
To solve these equations, subtract 4 from both sides to get these solutions.
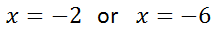
Here is our second example.
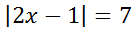
Now, we will bifurcate the absolute value equation.
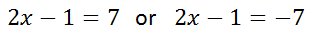
We will solve these equations. For the first step, we will add one to both sides of each equation.
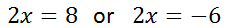
Next, we will divide each equation by two to gain our final solutions.
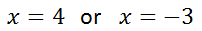
This link below will allow you to view an instructional video on this topic.
Use the quiz below to determine if you have mastered the lesson you have read.
Our next section will detail the steps needed to get the solution(s) for inequalities that contain absolute value.
| |
When we encounter an absolute value inequality, we must follow several algebraic steps. Those steps are outlined below.
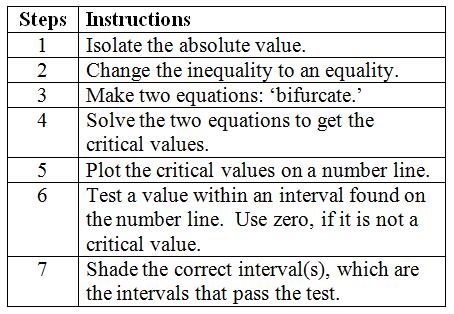
| |
The steps outlined within the last section will be utilized for the two examples below. Example 1:
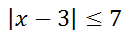
Step 1: It informs us to get the absolute value alone. The absolute value is already alone on one side. On to the next step... Step 2: It tells us to change the inequality to an equality. This gives us the following equation.
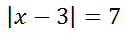
Step 3: We are told to make two equations, which is the bifurcation step.
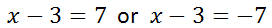
Step 4: We must solve the equations. We can solve the two equations by adding 3 to both sides. These are the critical values that we get.
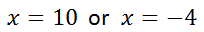
Step 5: We must plot the critical values. We must use solid points because the original problem partly contains equality.
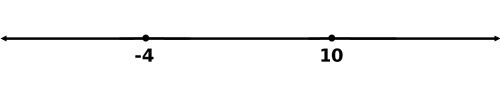
Step 6: Now we have to test a value that isn't a critical value. Since zero is not a critical value, it is a valid test value. Zero rests between our critical values.
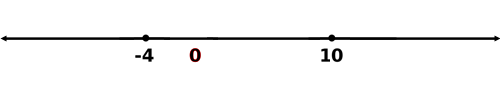
To test this value, replace the 'x' within the original problem to see if it produces a true expression, like so.
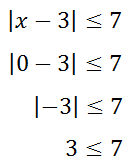
Since 3 is less than 7, our test value of zero produces a true response. Therefore, the interval between -4 and 10 is the interval to be shaded. Step 7: When we shade intervals, we usually shade either to the left and right of the critical values or we shade in between the critical values. Since the middle interval is a solution. We will shade that section. [Values within the other two intervals can be tested at the reader's leisure. Values within the left and right intervals produce false results.]
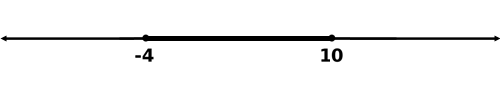
Besides a visual representation, we can represent the interval using inequalities. Since the solution is between -4 and 10, we can represent the interval using a compound inequality.
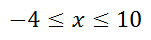
For the next example, the algebra will be shown but accompanied by less of an explanation.
Example 2:
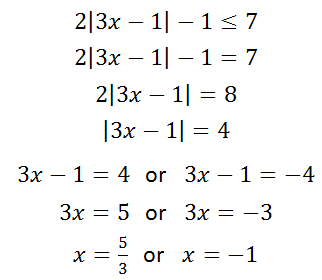
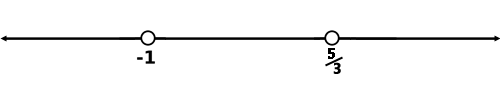
Check the value x = 0.
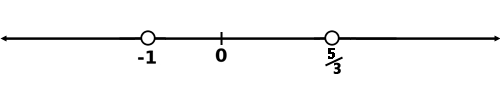
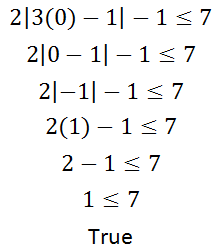
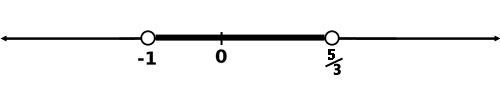
Therefore, this is the inequality that is the solution.
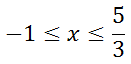
Use the video below to help understand this lesson.
Use this interactive quiz to determine if you understand the lesson. | |
This instructional video will explain how to use a graphing calculator to solve absolute value inequalities. This video utilizes a TI-Nspire calculator, but several other manufacturers make excellent calculators, too, like Casio, Datexx, and HP. There are also several websites that offer web-based calculators.
| |
Here is a video that can help you learn the lessons above.
| |
Use this interactive quiz to determine if you understand the lesson.
| |
The lessons below are related to solving absolute value inequalities.
| |
 ideo:
ideo:  uiz:
uiz:  esson:
esson: