Central Angle and Arc Relationship | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn the relationship between central angles and their respective arcs. Here are the topics within this page:
|
To grasp the relationship between angles and arcs within a circle, you first have to know what a central angle looks like. A central angle is an angle whose vertex rests on the center of a circle and its sides are radii of the same circle. A central angle can be seen here.
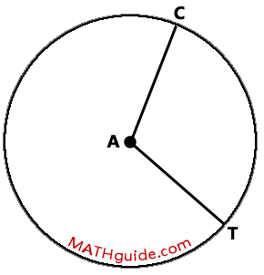
The diagram above shows Circle A. [A circle is always named by its center.] The central angle is angle CAT. Notice that point-A is the vertex of the angle, which is at the center of the circle. Also notice arc CT, which is the rim of the circle that connects point-C to point-T. Two segments of interest within the diagram would be two radii, segment AC and segment AT.
Within the next section, we will examine the relationship between a central angle and its arc.
| |
We will be looking at several situations that involve central angles and arcs. To understand these situations it would be helpful to grasp the different types of arcs that exist. The diagram below will display three different types of arcs and the central angles that intercept those arcs.
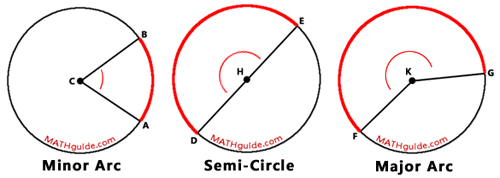
The diagram above shows three different types of arcs and central angles. The table below will describe minor arcs, semi-circles, and major arcs and their corresponding central arcs which are acute, straight, and reflex angles.

Within the next section, we will examine the relationship between a central angle and its arc.
| |
The relationship between a central angle and its opposite arc can be seen below.

This relationship will be demonstrated by viewing the examples below.
| |
Determine the measure of minor arc FW within the diagram that follows.
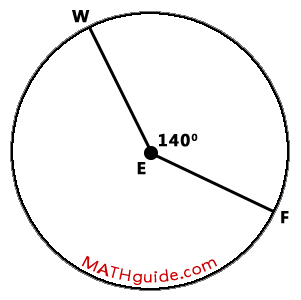
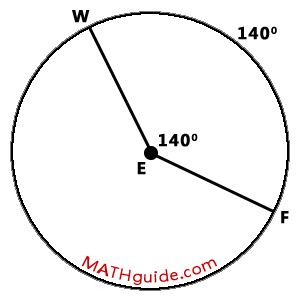
As can be seen within the diagram above, central angle FEW is 140 degrees. This means the arc it intercepts, arc FW, is equal to the same measure, which is 140 degrees.
| |
Determine the measure of angle FVN and major arc FUN within the diagram that follows.
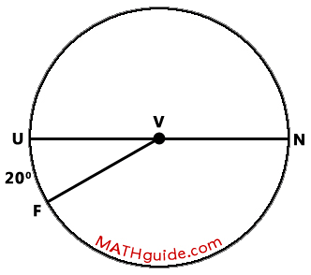
Chord UN travels through the center of circle V, which means it is a diameter. This also means that arc NU is half of a circle, which makes it 180 degrees in measure.
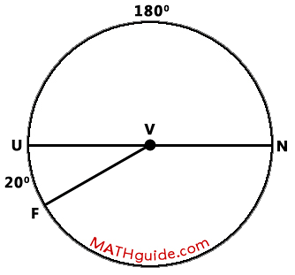
According to our diagram, arc FUN is equal to the sum of arc UF and arc NU. Since 20 degrees plus 180 degrees is 200 degrees, the measure of major arc FUN is also 200 degrees. Now, let us move toward the central angles within the diagram. Since arc UF is 20 degrees, central angle FVU is 20 degrees. Likewise, central angle UVN is equal to 180 degrees based upon the arc it intercepts.
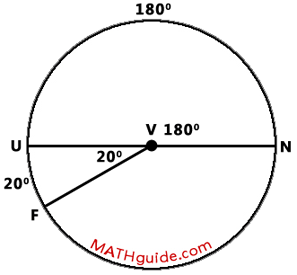
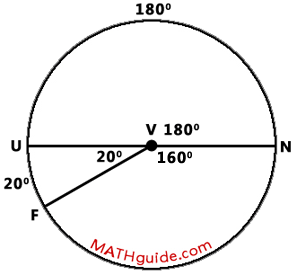
As we examine the diagram further, we can see that there is an angle relationship that is important to recognize: angle UVF + angle FVN = 180 degrees. Since angle UVN is 20 degrees, angle FVN has to be 160 degrees.
| |
View the following instructional videos.
| |
This quiz is designed to check for your understanding. | |
There are no activities at this time. | |
Here are related lessons to the central angle and arc relationship.
| |
 ideo:
ideo:  uiz:
uiz:  esson:
esson: