Basic Counting | ||
| ||
Introduction | ||
In this section, you will learn how to perform a variety of counting problems. Here are the sections within this lesson:
|
Counting sounds too primitive to have special meaning for high level mathematics. However, that thought could not be further from the truth. Just as counting sheep was important for ancient herders and livestock holders, counting is crucial for determining the number of possible outcomes of certain events or the likelihood of an event from occurring.
So, this lesson will look at different situations and develop strategies for counting them.
| ||||||||
Here is a common problem.
If Jim has five shirts and three pairs of pants, how many different combinations of clothes can he wear?
Here are all the different combinations Jim could wear: {Red Shirt, Grey Pants} {Red Shirt, Beige Pants}
{Black Shirt, Black Pants}
{White Shirt, Black Pants}
{Green Shirt, Black Pants}
{Purple Shirt, Black Pants} A quick tally tells us there are 15 combinations for Jim to wear. However, this process was a bit too difficult to do, especially if Jim acquires more clothing. So, there must be a more efficient method for counting and there is a better method. This takes us to our next section.
| ||||||||
A faster method for counting possible outcomes does exist, than was used above in our last section. The fundamental counting principle says this: If there is ‘m’ number of outcomes for one item and there is ‘n’ number of outcomes for another item, then there is ‘m x n’ number of outcomes total. We can use this principle for our problem above. If Jim has five shirts and three pairs of pants, how many different combinations of clothes can he wear? There are 5 outcomes for shirts and three outcomes for pants. So, this is how the fundamental counting principle works.
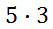
There are 15 total combinations for Jim to wear.
For the problems that follow, we will explore different real-life scenarios.
| ||||||||
When state government officials issue license plates, they have to make sure there are enough plates for the people who drive in their state. Each vehicle has to have its own unique plate. So, officials have to be able to count the number of plates it produces. Example 1: Here is a situation that an official has to count to determine the number of different plates that can be produced. Keep in mind, small case letters are never used on license plates. A certain state uses license plates that have six characters. The first two characters must be letters. The last four characters can be either letters or numbers. How many unique license plates can be made? To figure out this problem, we need to look at all the options for each character. Imagine this is a license plate. Each blank below represents a possible character on a plate.
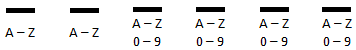
For letters A – Z, there are 26 characters. This means the first two characters have 26 outcomes each and the last four characters have 26 + 10, or 36 characters each. Using the fundamental counting principle, we get this set-up.
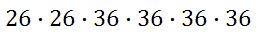
This is equal to 1,135,420,416. So, this license plate system is good for producing over 1.1 billion different plates for over 1.1 billion different plates. Example 2:
A certain state uses license plates that have five characters. The first two characters must be letters, but the letters O and Q cannot be used. [They look too much alike and cause problems for police officers.] The last four characters can be either letters (no Os or Qs) or numbers 1 – 9. [Zeros cannot be used because they look like Os to police officers.] How many unique license plates can be made? Here is a table that outlines our situation.
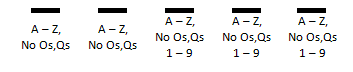
For letters A – Z without the Os and Qs, there are 24 characters. This means the first two characters have 24 outcomes each and the last three characters have 24 + 9, or 33 characters each. Using the fundamental counting principle, we get this set-up.
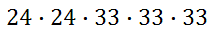
This is equal to 20,699,712. So, this license plate system is good for producing over 20 million different plates for over 20 million different vehicles.
| ||||||||
Many websites that keep track of data for users require a login and password. No two users can have the same login; so, it is important for website developers to create login systems that have a lot of possibilities to allow for a large number of users. This section will explain how to count the number of logins and the number of passwords a website may use. Keep in mind, that login and password data can usually contain both uppercase and lowercase letters and numbers. Some websites allow password data to contain special characters, like these symbols: @, #, %, !, $, +, -, and $. Here is our first problem. Example 1:
A certain website allows for eight characters for its password. The first character has to be a letter and the last character has to be a number. However, the middle six characters can be letters and numbers. How many different passwords can this system allow? Here is how this password system works – broken down by position.

Using the fundamental counting principle, we get this set-up.
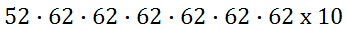
This login system will give us 29,536,122,503,680 unique logins! That is more than 29 trillion possible passwords, which is a sufficient number of passwords to keep data safe. Example 2:
A certain website allows for nine characters for its login. The first character has to be a letter and the last character has to be a number. However, the middle seven characters can be letters, numbers and special characters. How many different logins can this system allow? Here is how this login system works – broken down by position.

Using the fundamental counting principle, we get this set-up.
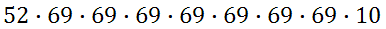
This login system will give us 3,872,103,691,346,280 unique logins! That is more than 3.8 quadrillion possible logins, which is more logins than any website will ever need.
| ||||||||
There are games that use dice, spinners, and other randomizers. In order to calculate probabilities, one must first calculate the number of total possible outcomes. Again, the fundamental counting principle is what must be used. First, we should take a look at various randomizers. Dice:

The above image shows two traditional 6-sided dice. Let it be known that there are dice that have 10-sides, 20-sides, and other numbers of sides. If a 6-sided die is rolled, these are the possible outcomes:
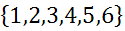
One can see there are six possible outcomes. If someone asked this following question, however; there is a different level of response.
For certain game, one has to roll a 6-sided die and an 8-sided die. How many possible outcomes are there? We will use the fundamental counting principle. There are 6 outcomes for the first roll and 8 outcomes for the second roll. So, this will tell us the answer.
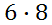
There are 48 possible outcomes. Spinners: Spinners are used in games to randomize moves on a board. They usually involve equally-spaced intervals that are numbered, like this diagram will demonstrate.
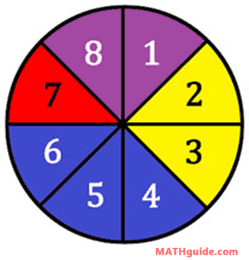
A played spins an arrow that is attached to the dial and a space is indicated by the pointer. When the spinner gets spun, there are eight possible outcomes:

We are going to take a look at a spinner problem related to counting.
For certain game, one has to spin the dial twice. Once it is spun for a number. Next, it is spun for a color. How many possible outcomes are there? There are eight numbers and there are four colors. We will use the fundamental counting principle.
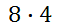
There are 32 possible outcomes.
| ||||||||
Try this video related to the lessons above.
| ||||||||
Try our interactive quizzes to determine if you understand the lessons above.
| ||||||||
Try these lessons, which are closely related to the lesson above.
| ||||||||


 ideo:
ideo:  uiz:
uiz:  esson:
esson: