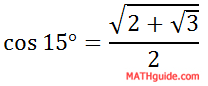Half Angle Formulas: Sine & Cosine | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn about half angle formulas for sine and cosine. Here are the topics within this page:
Before carrying on with this lesson, you must have knowledge of the double angle formulas. If necessary, review this lesson before moving on with the next sections. |
Here are the half angle formulas for cosine and sine.
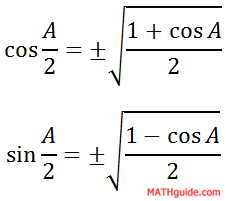
In the next two sections, these formulas will be derived.
| |
We will begin by looking at the Double Angle Formula for cosine.
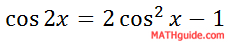
Solve this for cos x, like so.
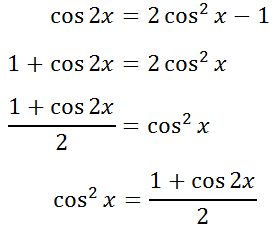
The last step to get the cos x alone on the left side, we need to apply the square root to both sides of the equation. In doing so, we must place a plus-minus sign on the right side of the equation.
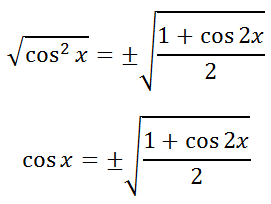
Let 2x = A, which means x = A/2. We can replace the x-variables with A/2, like so.
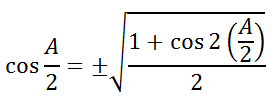
We can clean up the angle inside the square root to get the final half-angle formula for cosine.
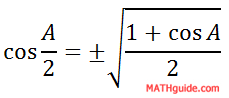
| |
Here is another Double Angle Formula for cosine.
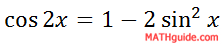
We will solve it for sin x by using simple algebra.
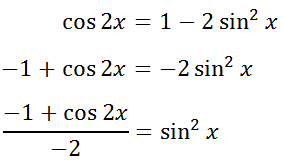
To simplify the left side of the equation, we can divide both the numerator and the denominator by -1. In doing so, both the numerator and the denominator will change to opposite expressions.
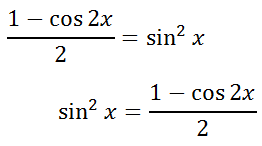
Now, we can take the square root of both sides, which requires a plus-minus sign.
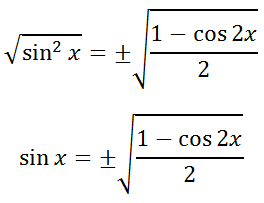
Like what was done in the section above for the cosine formula, let 2x = A, which means x = A/2. We can replace the x-variables with A/2, like so.
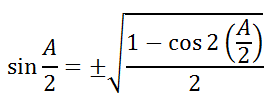
Cleaning up the angle expression under the square root, we get...
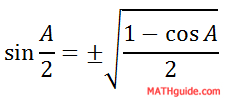
The formula above is the half-angle formula for sine.
| |
Say we had an angle like 15°. If we wanted the exact value of this angle using any trigonometric function, we could not calculate it. 15° is not a special angle. However, we can calculate double its value, which allows us to use a half-angle formula. We should look at a specific example, like this. Example: Calculate the exact value of cos(15°). We can calculate the cos(30°). So, we can use the half-angle formula for cosine. Start like this.
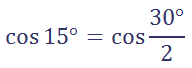
Writing our problem like this allows us to use the half-angle formula for cosine, like so.
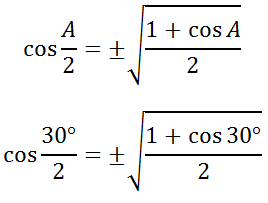
Using our knowledge of special angles, we know the exact value of cos(30°). We also know that the cosine of angles in the first quadrant are positive ratios. So, there is no need for the plus-minus sign.
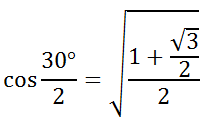
Getting a common denominator in the numerator to clean up the right side of the fraction, we get these next steps.
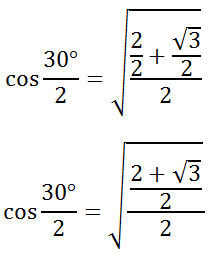
Cleaning up the complex fraction, we have to change the problem from division by 2 to multiplication by 1/2.
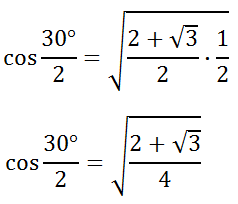
We can simplify the radical by using the square root on the numerator and denominator separately.
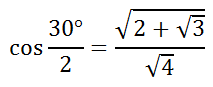
Our solution for cos(15°) is a ratio that contains a radical within a radical.
| |
Here are lessons that are related to the content above.
| |
 esson:
esson: