Logarithms | ||
| ||
Introduction | ||
In this section, you will learn a variety of properties and applications involving logarithms. Here are the sections within this lesson:
|
To answer the question, What is a logarithm? we have to understand exponents. Take this problem.
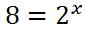
The 2 is called the base. The x is called the power, or exponent. The 8 is the answer one gets after raising the two to some unknown power. We can re-write this as a logarithm, like so.
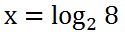
This means a logarithm is a variant of an exponential equation. It is a different way to express a problem involving exponents.
| ||||
To understand the properties of logarithms, one must first understand the properties of exponents. Logarithms are exponent problems that have been altered; so, understanding one helps to understand the other.
If you would like to review a detailed lesson on exponents, see our lesson called Power Rules of Exponents.
| ||||
Keep in mind the properties of exponents from the previous section. Understanding them will help with understanding logarithms and its properties. Assume we were given this logarithm expression.
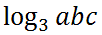
We can write this expression as follows instead.
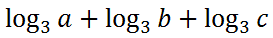
This is possible because logarithms are exponents and the property of dealing with a times b times c allows us to use the first rule of exponents. Multiplication and addition are linked. Similarly, let us examine this logarithmic expression.
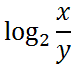
It can be written like this.
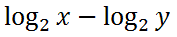
This is so because division and subtraction are linked, much like multiplication and addition are linked for exponents. See property two for the properties of exponents. Here are the properties of logarithms.
These two properties have been explained above. However, to get to a new property, let us take a look at this expression.
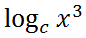
We can expand the expression, x-cubed.
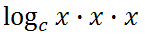
Using the first property, we get this progression.
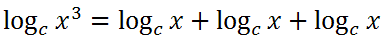
Using algebraic skills, we can combine logarithmic expressions by adding coefficients, which are all equal to one, like so.
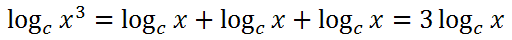
In short, it means we can make exponents coefficients, which is demonstrated below.
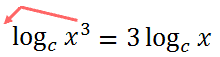
We see that the exponent tells us how many terms there would be; so, if the power was 'n'...
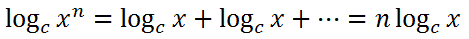
...because there would be 'n' number of terms. This is our third property of logarithms.
| ||||
There are exercises that ask students to either expand or contract problems that contain logarithmic expressions. We will explore several of them and use properties of logarithms to do so. Example One Expand this expression.
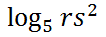
Using the first property of logs, we get this.
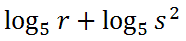
Now, we can use the third property of logs on the exponent.
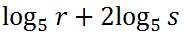
This is the final answer, because no further properties can be used.
Example Two Contract this expression.
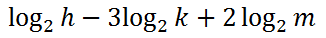
We are going to use the third property of logs to move the coefficients into the power positions.
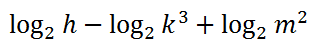
Let's use property two on the first two terms -- subtraction translates to division.
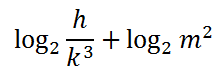
Next, we will use the first property. Addition translates into multiplication.
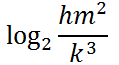
We are done with this problem.
| ||||
There are situations where scientists, like biologists, sanitary engineers, and physicists, need to solve problems that contain variable exponents. Using logarithms is best used to solve those problems. For instance, we should examine this problem. Example 1
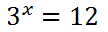
We will take the logarithm, base-10, of both sides.
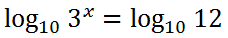
When we use the logarithm, base-10, we do not need to write the base. We will instead, write it without the base, because base-10 is assumed if it is not written.
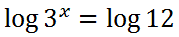
We can use the third property to bring the exponent in front of the logarithm, which is the reason why we are using logarithms for this problem.
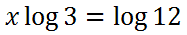
The ability to move the exponent in front, into the position of a coefficient, allows us to solve the problem. Now, we can use simple algebra. We can divide both sides of the equation by the log of 3, like so.
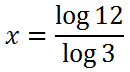
We can use a calculator at this point, if we are interested in a decimal approximation. Doing so gives us this value, using a TI-83+ calculator.
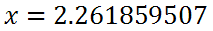
If we round this to the nearest hundredth, the '1' in the thousandth place tells us to simply round down to...
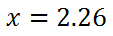
Example Two For this problem, only the steps will be shown.
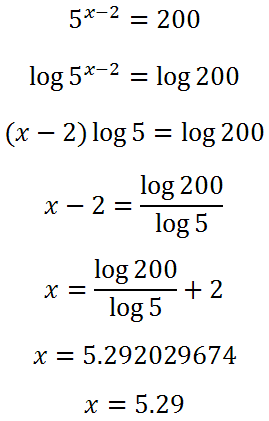
Notice how the third property was used from step #2 to step #3 above. The power, (x - 2), was moved from the position of exponent to coefficient.
| ||||
In order to demonstrate the need to understand logarithms, we will investigate two real world problems: one with bacterial growth and the other with radioactive decay. Problem One: Bacterial Growth
A certain strain of E coli bacteria (found in fecal matter) has a doubling rate of 30 minutes. If there are 100 E coli bacteria that are allowed to grow under ideal conditions, how long will it take to reach 1 million bacteria? Here is a table that demonstrates how quickly the bacteria are growing. Instead of dealing with minutes, the time has been incremented in half-hour steps.
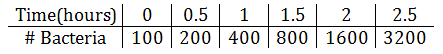
It can be seen that the cells are doubling not every hour, but every half hour. To reflect this doubling rate, we need to place a 2 next to our variable t because it doubles twice per hour and have a base of two due to the doubling nature of bacteria. This is the formula that captures the relationship above.
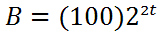
We will now use it to solve for time when the number of bacteria is equal to 1 million. This is the equation we must use to solve the problem.
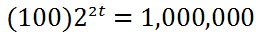
To start solving the equation, we divide both sides of the equation by 100.
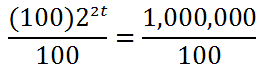
We get this result.
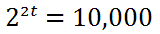
we have to take the log of both sides.
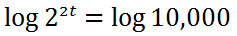
We are going to use the power property of logarithms, which allows us to take exponents and write them as coefficients.
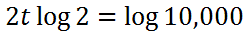
To solve for t, we must divide both sides by the log of 2.
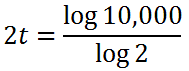
It looks like we have to also divide both sides of the equation by 2.
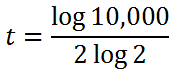
Plugging the right side into a TI-nspire CX yields this.
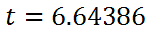
If we round it to the nearest hundredth of an hour, we get this final solution.
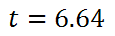
A slight calculation involving 0.64 hours would tell us we would reach 1,000,000 bacteria in 6 hours, 38 minutes, and 24 seconds, if the bacteria behaved perfectly exponentially throughout the entire time. Use the quiz below to determine if your knowledge of bacterial growth is correct. The general formula for bacterial growth is...
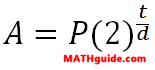
...where the P-value is the initial cell population, the A-value is the final cell population, the t-value is time, and the d-value is the double rate of the bacteria within an optimum medium.
Problem Two: Radioactive Decay Radioactive isotopes degrade over time. While they degrade, they give off energy. Some of that energy can be very dangerous to living organisms. Some of the lower levels of energy can be used by medical professionals to help people who are suffering from cancer. The isotope Plutonium-239 is used for the production of nuclear bombs and it is part of the composition of nuclear waste. It has a halflife of 24,000 years. This means it takes 24,000 to lose half of its energy. We are going to use this isotope for the following problem.
16 grams of Plutonium-239 were produced by a foreign nation to create a nuclear bomb. How long would it take for the plutonium to degrade to 0.05 grams? To gain a better understanding how the energy degrades over time. Let us examine a table that describes this slow process.
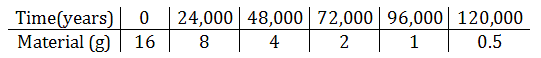
The formula that encapsulates this table of information is this.
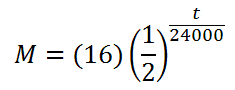
We want to know when the material will degrade to 0.05 grams. This means we must use that value for M.
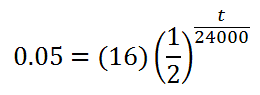
To solve this equation, we need to divide both sides by 16.
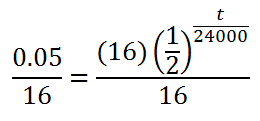
This gives us this equation.
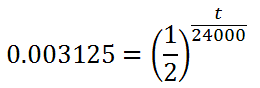
The variable is part of the exponent. In order to move the variable out of that position, we will use Logarithm Property Three. We will need to take the log of both sides, first.
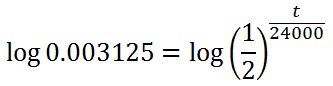
Now, we will move the exponent in front of the log, using the third property.
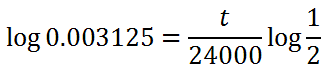
Now, we will divide both sides by the log of 1/2. For the sake of simplifying this equation, we can replace the 1/2 with 0.5.
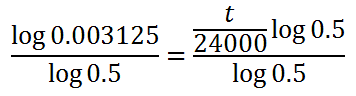
This gives us much closer to our final goal.
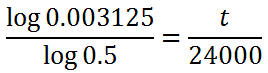
Our next step involves multiplying both sides by 24,000.
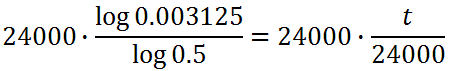
This is what needs to be placed into a calculator.
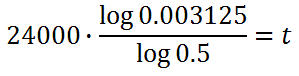
Placing it into a calculator, we get this value.
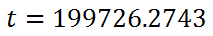
Rounded to the nearest hundredth, we get this value.
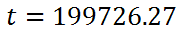
It is clear that nearly 200,000 years is a long time. Some isotopes in nuclear materials last quite a long, long time. The general formula for dealing with radioactive decay is...
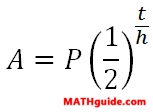
...where the P-value is the initial mass, the A-value is the final mass, the h-value is the half-life of the given radioactive substance, and the t-value is time. Use the instructional video and interactive quiz below to learn and test your knowledge about radioactive decay.
Problem Three: Human Population Growth There are animal population problems that utilize a special formula. This formula containing the constant 'e' is commonly used for all sorts of population problems. A = Pert The P-value is the initial population. The 'e' is a constant. Like pi, it goes on forever with no pattern. It is approximately equal to 2.72. The r-value is the rate, written as a decimal number even though people speak of rates in terms of percents. The t-value stands for time.. Finally, the A-value stands for the final population amount after t-units of time pass. The video below will explain how to use the formula to solve two word problems.
| ||||
Watch our instructional videos regarding these lessons above.
| ||||
Try our interactive quizzes to determine if you understand the lessons above.
| ||||
These are the activities related to the lessons above.
| ||||
These lessons are related to the lesson above.
| ||||
 ideo:
ideo:  uiz:
uiz: 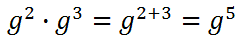
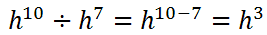
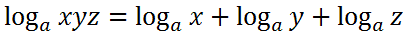
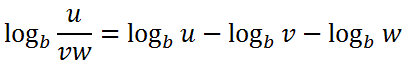
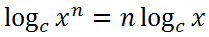
 ctivity:
ctivity:  esson:
esson: