In this section of MATHguide, you will learn about proportions. Here are the topics within this page:

• Ratios
• Proportions
• Solving Proportions
• Instructional Videos
• Interactive Quizzes
• Related Lessons

    To thrive within the world of proportions, we first need to understand what a ratio is. A ratio is a comparison of two values. We could compare a rectangle's width to its height. We could compare the sticker price of a car versus our yearly earnings. As can be seen, these ratios have meaning.

    If a rectangle has a small width but a large length, it can be seen that the rectangle is long and skinny, like this rectangle.

    However, if a rectangle's length and width are close in value, the rectangle is closer to looking like a square.

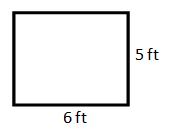
    Likewise, when we compare the cost of a car to our yearly salary, the closer the two values match, the more unaffordable the car becomes. If a car is a $5,000, but we make a yearly salary of $200,000, such a car's purchase would cause less impact on our life. A 40th (¹/₄₀) of our yearly salary is a cost that would be easy to afford, unlike a $100,000 car, which would be half (¹/₂) of our salary.

      ideo: Proportions

    When we think of ratios of values, we usually think of fractions. A 2:3 ratio, spoken as " a two to three ratio," can be written as a fraction: two-thirds or...

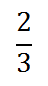
    Proportions are simply described as two equal ratios like this example.

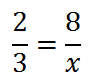
    When ratios were written in old textbooks, fractions were impossible to write. So, they were written like this.

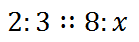
    It was read as "two to three to eight to x."

      ideo: Proportions

    To solve for the x-value, students multiplied the means and extremes and set the products equal to each other. The means are the inside two values and the extremes are the outside values.

    This equates to...

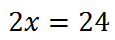
    For proportions, this can be viewed as "cross-multiplication."

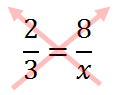
    This also shows ...

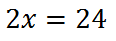
    Continuing along using algebra, we get this.

      ideo: Proportions
      uiz: Proportions

---

    Here is another proportion that we will solve.

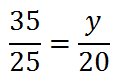
    Again, we multiply means and we multiply extremes. which can also be seen as cross-multiplication.

      ideo: Proportions
      uiz: Proportions

    Here is an instructional video that explains all the aspects of proportions.

      ideo: Proportions

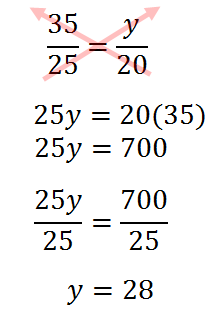
    Try these quizmaster to determine if you understand how to solve proportions.

      uiz: Proportions
      uiz: Proportions 2
      uiz: Proportions 2 with Help
      uiz: Proportions 3

      esson: Reducing Fractions
      esson: Geometry Proofs
      esson: Similar Figures
      esson: Dilations
      esson: Areas and Lengths of Similar Figures
      esson: Volumes and Lengths of Similar Solids