Angle Between Two Vectors | ||
| ||
Introduction | ||
This lesson page will explain how to calculate the angle between two vectors. Here are the sections within this lesson page:
|
In order to understand how to calculate the angle between two vectors, you must have learned several other concepts and skills. Make sure you are familiar with the content below before proceeding with this lesson.
As a side note, this lesson uses two notations for vectors. If a letter is bold or it has an arrow ( → ) above it, it is a vector. For instance, these two symbols both mean vector w.

| |
We need to know how to calculate the angle between two vectors for numerous reasons. Vectors are all around us. Vectors are the forces that are acting on beams and other supports within structures. Vectors are used to represent wind, pressure, humidity, and many conditions for predicting weather patterns and climates.
The air that flows around an aircraft’s wing, the fluid that flows within a pipe, and several other situations are modeled using vectors. These vectors help researchers create aircraft that is fuel efficient and pipes that contain extreme pressures.
When two forces interact, the angle between those forces is important for determining the resulting force.
| |
The equation for finding the angle between two vectors, u and v, is this.
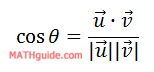
This equation is not a simple one. It involves a trigonometric function, the dot product of two vectors, and the magnitude of two vectors.
The examples below will explain, in detail, how to use the equation to find theta, the angle between two vectors.
| |
Let us start with two vectors, u and v, so that we can determine the angle (in degrees) between the two vectors.
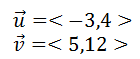
The equation requires us to determine the dot product of the two vectors.
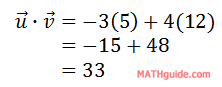
The equation requires us to calculate the magnitudes of the vectors; so, here are their magnitudes.
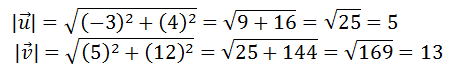
Now, we can place this information into the equation, like so.
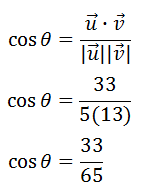
To solve for the angle, theta, we must use the inverse cosine or arccosine, like so.
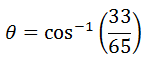
If your calculator is set for degrees, the angle rounded to the nearest thousandth is…
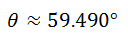
Use these resources to help yourself learn more about the angle between two vectors.
| |
Here is another example. So, here are two new vectors, u and v. We will again determine the angle (in degrees) between the two vectors.
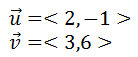
Here is the dot product between the vectors.
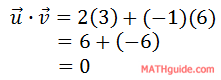
Here are the magnitudes of the two vectors.
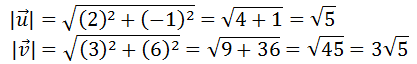
We can plug in the values into their appropriate places within the equation.
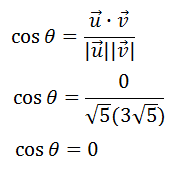
This problem does not require the use of a calculator, for two reasons. The first is that knowledge of the unit circle should tell us that the cosine of 90 degrees is equal to zero. The second reason is that the dot product being equal to zero means that the vectors are orthogonal. This also means the angle between them is 90 degrees.
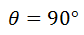
See our lesson on Orthogonal Vectors. Use these resources to help yourself learn more about the angle between two vectors.
| |
This video reveals what the formula is, provides two examples, and explains the graphical representation.
| |
Try this quiz to see if you understand how to find the angle between two vectors. | |
Try these lessons, which contain more information on vectors.
| |
 esson:
esson:  uiz:
uiz:  ideo:
ideo: