Limits: by Conjugates | ||
| ||
Introduction | ||
This lesson page will inform you how to find limits of certain rational functions that contain square roots. The method that will be taught for this situation will be a method by conjugates. Here are the sections within this page: If your knowledge of conjugates and/or ability to reduce rational expressions is weak, review this material before proceeding.
|
Here is a complicated limit.
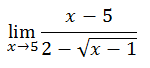
We can try substituting the value 5 into the expression, like so.
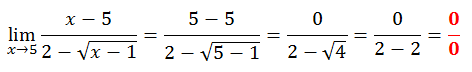
This result is a huge issue because it is illogical to have a denominator equal to zero. See this MATHguide video to learn why this is so.
If we get a zero in the denominator, it means the result is indeterminant. It means we know nothing about the limit and that we have to try a different strategy. So, we are going to look at conjugates. The denominator of the original problem is this.
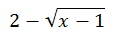
It has a conjugate, which is this.
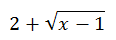
We are going to multiply the numerator and the denominator of the original rational expression by this conjugate. Why? Doing the algebra will reveal how it will simplify the problem.
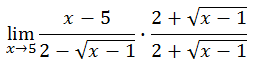
There is a great deal of algebra to do, like doing the double distributive property when we multiply the denominators.
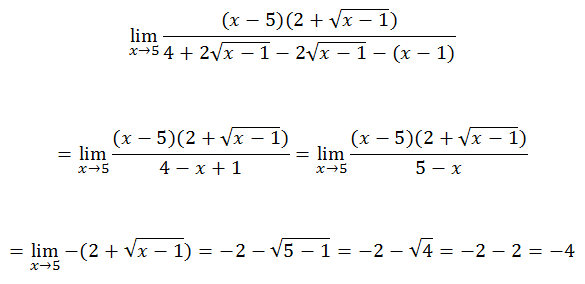
Here is another example.
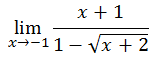
The conjugate of the denominator is…
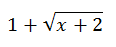
We will multiply the numerator and the denominator by this conjugate, like so.
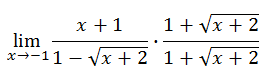
The remainder of the problem requires a number of algebraic steps, shown below.
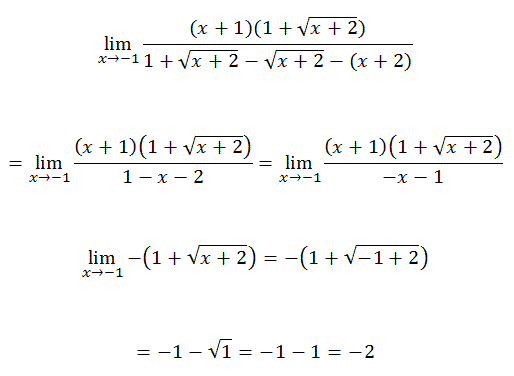
| |
Try this instructional video to learn this lesson.
| |
Try this interactive quizmaster to determine if you understand the lesson. | |
Try these lessons, which are related to the sections above.
| |
 ideo:
ideo:  esson:
esson:  uiz:
uiz: