Literal Equations | ||
| ||
Introduction | ||
This lesson page will inform you how to solve literal equations, which is a STEM (Science, Technology, Engineering, and Mathematics) topic. Here are the sections within this lesson page:
|
If you want to know what a literal equation is, consider this well known equation.
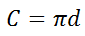
This equation is the relationship between the circumference of a circle with its diameter. The equation indicates how to determine the circumference of a circle -- by multiplying its diameter and the value pi. However, what if we knew the circumference of a circle and wanted to know its diameter? It would be helpful to know how to calculate the diameter by having a better equation. If we were able to solve the equation for the d-value, the equation would be more handy. The process of rearranging terms and performing mathematical operations on an equation to solve for a different variable is called solving a literal equation. Likewise, the area of a square is written like so.
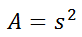
This means the area of a square is equal to the length of its side times itself. What is the length of a side of a square if you know the area of that square? The answer to that question demands that we are able to solve a literal equation to get the s-value alone. Being able to solve literal equations like the ones above is required to fully understand and utilize all mathematical relations, like those found within several science disciplines.
The next section will continue down that road and demonstrate how to solve literal equations.
| |
Let us examine a few equations to get a feel for how to solve literal equations. Example 1: Solve for the diameter.
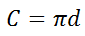
To get the letter-d alone, we need to find a way to remove the pi from the right side. Since pi is being multiplied to the letter-d, the inverse operation would be to divide by pi. So, dividing both sides by pi gives us this.
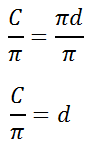
The diameter of a circle is equal to its circumference divided by pi. Example 2: Solve for the side.
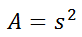
The equation is s-squared is equal to area. The inverse of squaring is square-rooting. So, we need to take the square root of both sides to simplify the right side of the equation, like so.
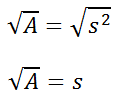
This tells us that the square root of a square's area is equal to the length of its side. Try this quizmaster to determine if you understand basic literal equations. | |
Here are more difficult problems to consider. Example 1: Solve for the length.
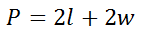
This formula indicates exactly what to do with the length and width of a rectangle to gain its perimeter. On the other hand, if we want to get the length -- the letter-l alone -- we have to first get the 2w term to the opposite side of the equation. Since we are adding 2w, the inverse is to subtract 2w from both sides, like so.
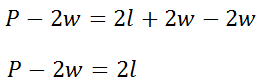
Now, to cancel the two that is being multiplied to the l-variable, we need to divide both sides of the equation by two.
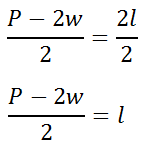
This equation now tells us how to use the perimeter of a rectangle given its perimeter and width. Example 2: Solve for the height.
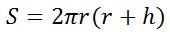
This equation tells us how to find the surface area of a cylinder using its radius and height. Let's use the equation to solve for h, the height of a cylinder. First, we need to do the distributive property.
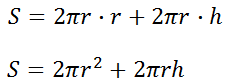
Now, we need to get the h-term alone, which means canceling the term with the r-squared. So, we need to subtract that term from both sides.
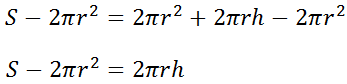
For our last step, we need to divide both sides of the equation by 2(pi)r to get the h-variable alone, like so.
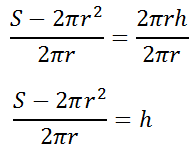
This tells us how to determine the height of a cylinder given its surface area (S) and radius (r). The following quizmaster contains six moderate level problems. Give it a look to see if you understand how to manipulate literal equations. | |
Try these lessons, which are related to the sections above.
| |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  uiz:
uiz: