Properties of Parallelograms | ||
| ||
Introduction | ||
This lesson page will inform you about the properties of parallelograms. Here are the sections within this lesson page:
Before reading on with the sections in this lesson, we recommend that you first review this lesson:
|
A parallelogram is a quadrilateral that has opposite sides that are parallel.
Since a parallelogram is a quadrilateral, a parallelogram has all of the properties of a quadrilateral in addition to properties unique to itself. The sections below will address its unique properties.
| |
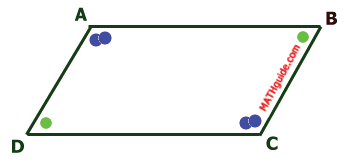
Starting with the definition of a parallelogram, several properties can be discovered. We will see that the sides have an interesting property. Given parallelogram ABCD with diagonal AC.
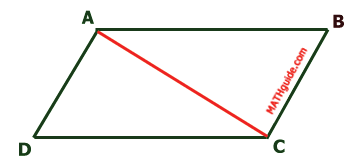
Since segments AD and BC are opposite sides, they are parallel by definition of a parallelogram. This means angle BAC is congruent to angle ACD because alternate interior angles are congruent for parallel lines.
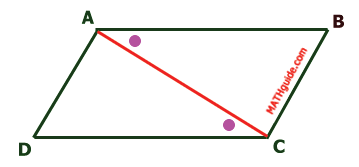
Likewise, AD is parallel to BC by definition of parallelogram. Angle CAD is congruent to angle ACB because alternate interior angles are congruent when lines are parallel.
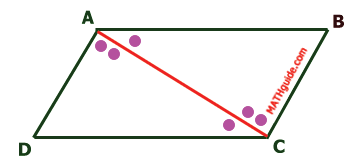
Segment AC is congruent to itself by the reflexive property.
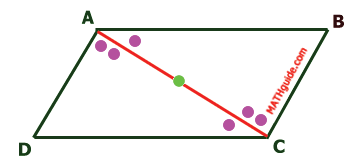
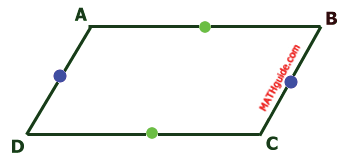
This means triangle ABC is congruent to triangle CDA by ASA. Since the triangles are congruent, corresponding parts of congruent triangles are congruent (CPCTC). This means segment AD is congruent to segment CB and segment AB is congruent to segment CD. In other words...
Congruent for Parallelograms
| |
The previous section showed that triangle ABC is congruent to triangle CDA.

This means angle D is congruent to angle B by CPCTC. It was also shown in the last section that two pairs of angles were congruent. For ease of discussion, these angles will be marked like so.
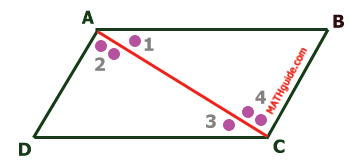
If two pairs of angles are congruent then their sums have to be congruent.
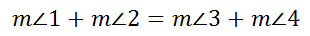
Since the measure of angle 1 plus the measure of angle 2 is equal to the measure of angle BAD and measure of angle 3 plus the measure of angle 4 is equal to the measure of angle DCB, we can say that angles BAD and DCB, which are opposite angles, are congruent. We could easily prove the other pair of opposite angles are also congruent. We would have to draw diagonal BD and run through the same pairs of congruent alternate interior angles. For brevity, it will be skipped. This means... Congruent for Parallelograms
| |

By definition of a parallelogram, opposite sides are parallel. If line DC is a transversal for parallel lines AD and BC, then angle D and angle C are same side interior and therefore must be supplementary angles. We could make an equal argument for any two consecutive angles because opposite sides are parallel and there is a side (transversal) joining those parallel sides. This means...
Supplementary for Parallelograms | |
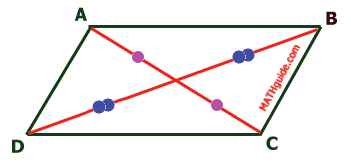
We determined that angles 1 and 3 are congruent because they are alternate interior angle for parallel lines AD and BC. Within the following diagram, both diagonals have also been drawn.
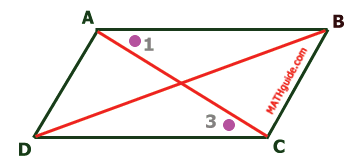
We know that opposite sides are congruent (see section Property: Opposite Sides); so, segment AB is congruent to segment CD.
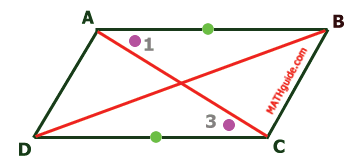
Another property of intersecting lines is that vertical angles are congruent.
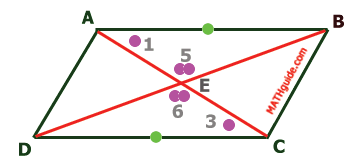
This means triangle BAE is congruent to triangle DCE by AAS. Since the triangles are congruent, then segment DE is congruent to segment BE and segment AE is congruent to segment EC by CPCTC. This also means diagonal BD bisects diagonal AC and vice-versa. Better said...
Bisect Each Other
| |
Review these related lessons
| |
 esson:
esson: