Parabola Characteristics | ||
| ||
Introduction | ||
In this section, you will learn about the characteristics of parabolas. Here is a list of the sections within this webpage:
| ||
A parabola is a mathematical shape that is used for determining the curvature of telescope lenses, the path of objects as they fly through the air, and the shape of satellite dishes. This means telescopes could not be made without them. Airborne objects would not be understood and satellite television would be impossible.
Clearly, parabolas are important and knowledge of them is vital to our technological society.
| ||
There are several key characteristics of a parabola. These characteristics include:
The rest of this lesson will inform you of these characteristics.
| ||
The x-intercept(s) of a graph can be found by looking at the x-axis. Wherever a curve crosses the x-axis, a x-intercept exists. Below is a parabola that has one negative and one positive x-intercept.
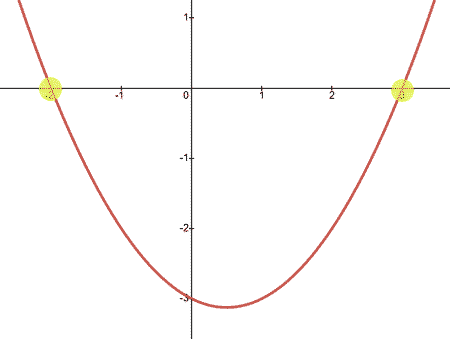
The parabola above has an x-intercept at (-2,0) and (3,0). Notice that x-intercepts always have a y-value of zero. This is why x-intercepts are sometimes referred to as zeros.
| ||
The y-intercept is the location where a curve crosses the y-axis. The parabola below has a positive y-intercept.
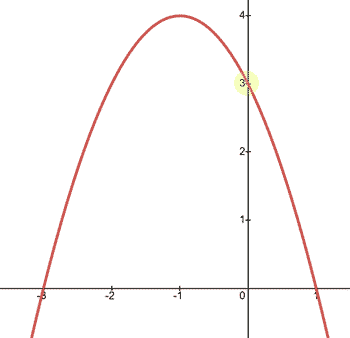
The parabola above has its y-intercept at (0,3). All y-intercepts have an x-value equal to zero.
| ||
Parabolas are u-shaped curves. If a parabola's branches go up, the concavity of the parabola is said to be 'concave up.' If a parabola's branches point downward, we say the parabola is 'concave down.' The parabolas below demonstrate this characteristic.
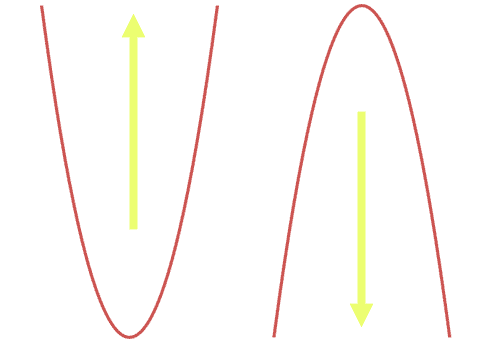
Looking at the parabola above, we see the left parabola is concave up and the right parabola is concave down.
| ||
When a parabola has a concavity that is up (the branches go up), the parabola has a minimum point. Conversely, when a parabola has a concavity that is down (the branches go down), the parabola has a maximum point. The diagram below shows this.
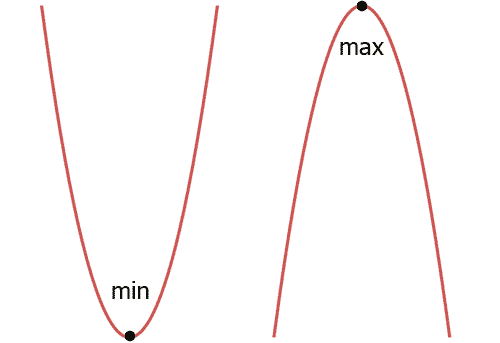
Locating the vertex of a parabola is important. The parabola below shows a vertex that is the minimum point.
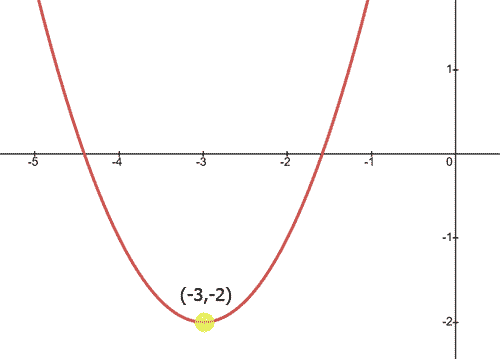
The parabola shown above has a vertex located at (-3,-2).
| ||
When a parabola is concave up or concave down, it has a line of symmetry that is a vertical line. This vertical line slices the parabola down its center. The parabola below will show this.
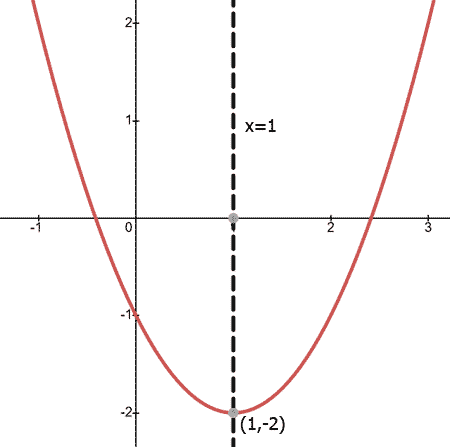
The parabola above has a vertex at (1,-2). The line of symmetry passes through the vertex as it will for all lines of symmetry. The equation of the line of symmetry for this parabola is x = 1 because all the points that are on the line of symmetry have a x-value equal to 1.
| ||
| ||
 esson:
esson: