Average Velocity | ||
| ||
Introduction | ||
This lesson will explain how to determine the average velocity of a situation that involves two different speeds over the course of a journey. Here are the sections within this lesson:
This lesson involves the use of the relationship between distance, rate and time along with rational expressions. If you find your skills in these areas need assistance, please use these lessons.
|

A dog runs directly from point A to point B at a rate of 5 feet/second. The dog then runs directly from point B back to point A at a rate of 14 feet/second. What is the average velocity of the dog? This problem appears – on its face – to have a simple solution. One could wrongly assume we could simply take the average of these speeds. However, that calculation is incorrect. The reason why the calculation is wrong is that it assumes the dog travels the same distances in the same amount of time. When the dog is traveling faster on its return journey, the dog covers the distance in a shorter amount of time. This means the two rates cannot be weighted equally.
To digest this view, we need to look at the definition of average velocity and see how the mathematics works.
| |
Here is the definition of average velocity.
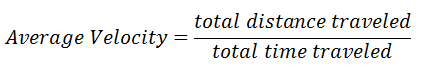
| |
Let us return to the original problem. A dog runs directly from point A to point B at a rate of 5 feet/second. The dog then runs directly from point B back to point A at a rate of 14 feet/second. What is the average velocity of the dog?

The total distance can be mathematically represented, even though the distance from points A to B is unknown. Algebra lets us label things using variables. So, we label the distance as ‘d’. This means the total distance is d (one distance from A to B) + d (the distance from B back to A) or 2d.
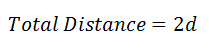
Determining the time spent traveling is not as simple. We have to use the relationship between distance, rate, and time. Here is the calculation done for each part of the journey.

Now we can see the total time as the sum of those two individual times. We have to take the time it takes to go from A to B and add it to the time it takes to go from B to A, like so.
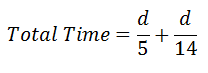
Returning to the definition of average velocity, we can put the total distance and total time together.
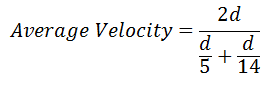
The rest of this is algebra, shown below.
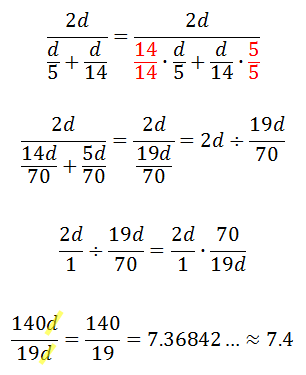
We can conclude the average velocity of the dog for the entire journey is approximately 7.4 ft/sec. Now, try our quizmaster to check for understanding.
| |

A lion runs directly from point A to point B at a rate of 35 feet/second. The lion then runs directly from point B back to point A at a rate of 20 feet/second. What is the average velocity of the lion? We will call the distance from A to B equal to the variable d. This means the total journey from A to B and then back to A is 2d. This is the total distance traveled. Next, we need to calculate the time it takes the lion to travel both legs of the journey.

The average velocity requires us to take the total distance traveled and divide it by the total time traveled, like so.
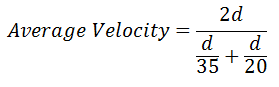
The algebra we must do to simplify this expression is shown below.
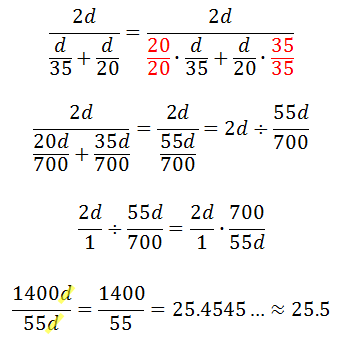
This means the average velocity of the lion over its total trek is 25.5 ft/sec. Try our quizmaster to check for understanding.
| |
Try our interactive quiz to determine if you understand the lesson above.
| |
Try these lessons, which are closely related to the lesson above.
| |
 esson:
esson:  uiz:
uiz: