Polynomial Models | ||
| ||
Introduction | ||
In this section, you will learn how to calculate the equation of a line using the point-slope formula. Here are the sections within this lesson:
|
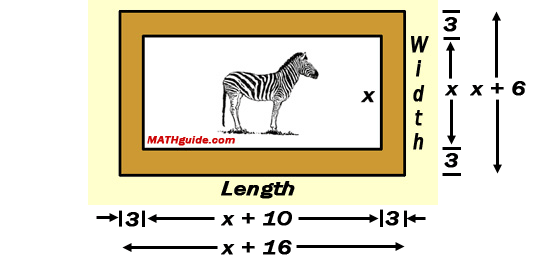
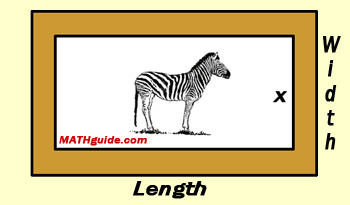
There are physical situations that require us to represent lengths, areas, volumes, and other situations (see our Flight of a Projectile lesson) using polynomials. Polynomials naturally arise because we often have to represent unknown quantities as variables, using 'x.' A math problem that used to receive a lot of attention in math text books was the picture frame problem. It appears to be coming back to the classroom due to its inclusion within the initial stages of the Partnership for Assessment of Readiness for College and Careers (PARCC) exam. [See our lesson on PARCC Exam Problems and Solutions.] Here is what the picture frame problem looks like.
To solve this problem, we need to find an expression for the length of the picture. However, we only know the relationship between the width and the length and we do not know how long the width is. We do know '[t]he picture is 10 inches longer than it is wide.' So since the width is represented by the x-value, we have to add 10 to it to get a length that is 10 inches longer than the width. This makes the length of the picture 'x + 10,' as is shown below.
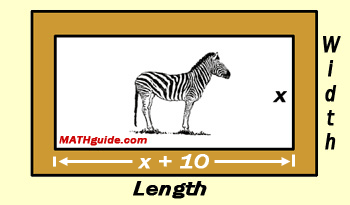
Next, we will come up with an expression for the length of the frame. Keep in mind the frame is 3 inches wide, as shown below.
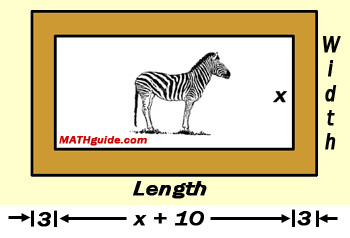
Now, we need to come up with an expression for the frame's length. We need to take the length of the picture and add 3 for the left side of the frame and another 3 for the right side of the frame, like so.
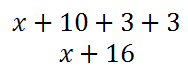
This can now be represented within the diagram.

Let us now calculate the area of the picture. We know area can be calculated as length times width. So, the area must be...
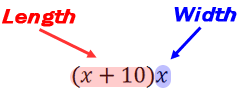
Let us now calculate the area of the frame and the picture. Keep in mind that the width of the frame is...
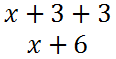
We know area can be calculated as length times width. So, the area must be...
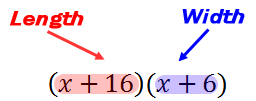
Try our quizmaster to test your skills. | ||
These resources will demonstrate how to calculate the maximum volume of an open box when congruent squares are cut from a rectangular-shaped piece of cardboard.
| ||
Here are videos that uses a polynomial model.
| ||
Try our interactive quiz to determine if you understand the lesson above. | ||
Here are activities for the Open Box problem.
| ||
Try this lesson, which is closely related to the lessons above.
| ||
 uiz:
uiz:  ctivity:
ctivity:  ideo:
ideo:  esson:
esson: