Continuity | ||
| ||
Introduction | ||
In this section, we will examine the concept and skill of continuity. The sections within this lesson are: Before progressing within this lesson, it is important that you understand several other concepts and skills. Please review these lessons, if necessary. |
Continuity can be explained easily by looking at the graph of a function. If the graph of a function can be drawn without lifting one’s pencil from the paper and be drawn with one motion, it is continuous along across the function. Here are some examples.
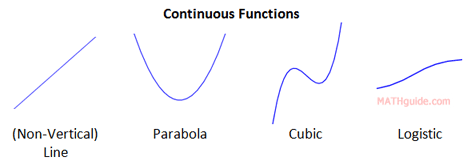
Here is an example where we have to be careful.

This function is not continuous because it has two “branches,” which prevents it from being sketched with one motion of a pencil.
The notion of continuity requires formal mathematics. This leads us to its definition.
| |
Continuity has a mathematical definition with two parts. Here it is.
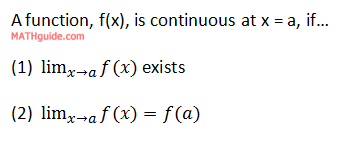
The definition only looks at a specific point, x = a, and does not analyze the entire function we happen to be examining.
The definition is thick, which means it needs to be unpacked with diagrams, explanations, and examples.
| |
Here are three types of discontinuities. They are easy to recognize when we see them.
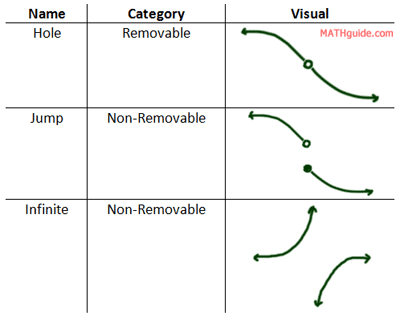
For each of the above situations, the function has a discontinuity. For the hole, it appears as though someone removed a point from the function. This is why it is called removable discontinuity. The other situations are not so simply explained, which is why they are categorized as non-removable. When testing for continuity, look for these cases. If you are testing a function at an x-value where one of these three situations occurs, you will know the curve is not continuous at that x-value.
Look at the examples below to gain more clarity on continuity.
| |
Here is a function we can examine for the purposes of continuity.
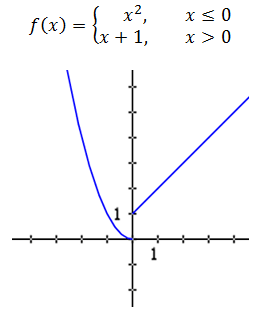
The function f(x) is continuous at all points except at x = 0. “Why is that?” you may ask. Look at the limits, which is the first condition of continuity. The limit from the left says this.
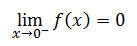
The limit from the right says this.
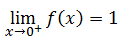
Since the left and right limits are different, it means the double-sided limit does not exist.
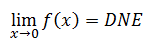
So, the function f(x) is not continuous at x = 0. This matches the visual check for discontinuity. However, take any other x-value in this function, say x = 1, and look at its test for continuity. Condition number one says to look at its left and right limits.
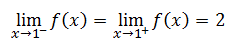
This means the double-sided limit exists.
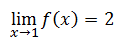
To test the second condition of continuity, we need to evaluate the function at x = 1. At x = 1, we use the right branch of the function, like so.
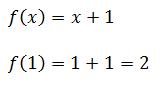
Since the limit at x = 1 is the same as evaluating the function at x = 1, this function passes the continuity test at x = 1.
| |
Here is another function.
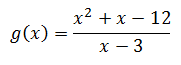
Is this function continuous at x = 3? If we plug this in to a calculator to graph it, we get a non-vertical line. Your instinct may tell you that this function g(x) is continuous. However, the calculator is not telling you something important about the curve. If x = 3, the denominator becomes zero. So, this curve is a line, but it has a hole at x = 3. Here is its graph.
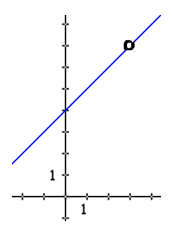
To determine if it is continuous, we can examine the definition for continuity. It passes the first part because the limit does exist.
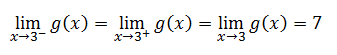
However, the second part of the test for continuity is an issue. The reason for that is because the function does not exist when x = 3. That is why there is a hole in the graph. All the other values for x exist except 3, which is why we removed it from the graph. So, this function fails the test for continuity at x = 3. If we look over the visual check for continuity, we see that discontinuities occur where there are holes in the graph. This confirms our conclusion that the function is discontinuous at x = 3.
| |
Here is a function.
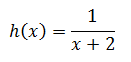
Is h(x) continuous at x = -2? Here is the graph of the function. We can use it to inspect the graph at x = -2.
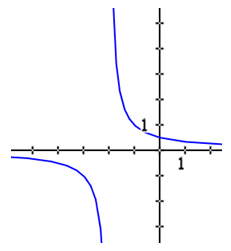
Look at the left limit as x approaches -2.
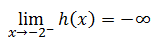
Look at the right limit as x approaches -2.
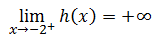
Since the left limit is different than the right limit, the limit does not exist. This means the function h(x) fails the first part of the limit test, which means the function is not continuous at x = -2. This conclusion is verified by inspecting the chart for visual discontinuities. The function h(x) has an infinite discontinuity at x = -2.
| |
Try this instructional video to learn this lesson.
| |
 esson:
esson:  ideo:
ideo: