Parabola in Factored Form | ||
| ||
Introduction | ||
In this section, you will learn about parabolas in factored form. Here is a list of the sections within this webpage:
| ||
A parabola is in factored form when it looks something like this.
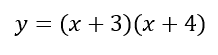
This particular parabola has two binomials that are being multiplied together.
| ||
If we were to graph the parabola...
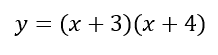
...this is what we get.
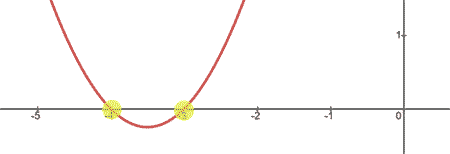
Notice that the parabola has x-intercepts at (-4,0) and (-3,0). Looking at the equation of the parabola, we could have known this by looking at its factors.
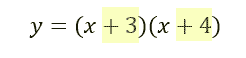
The factors and the x-intercepts form a simple relationship. The factors and the x-intercepts are opposite in value.

So, we can use this relationship in reverse. If we wanted a parabola to have x-intercepts at (-1,0) and (5,0), we would need to form factors that are opposite those x-intercepts, like so.
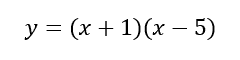
This is the graph of the parabola.
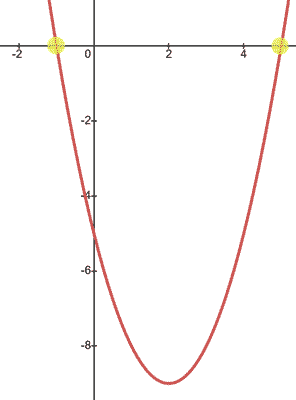
| ||
We see the graph of the parabola from the last section has branches that point up. This means the parabola is concave up. The reason is because of the leading number of the parabola. Although there was no number shown, we know there is a hidden factor of one.
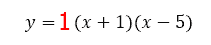
If the leading number were to be negative, we would gain a parabola that is concave down. Here is a parabola with the same x-intercepts but it is concave down.
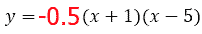
The graph of the parabola can be seen below.
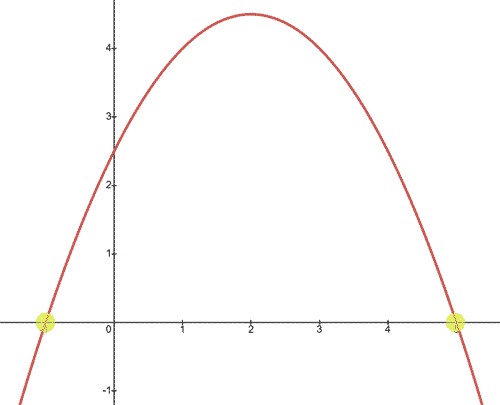
Observe the x-intercepts; they have not changed. Only the concavity changed.
| ||
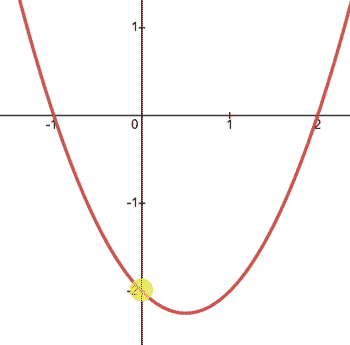
Here is the graph of a parabola.
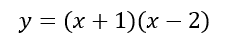
The graph passes through the y-axis at (0,-2). If we wanted to locate this point without graphing the parabola, we can by using its equation. A parabola will always pass through the y-axis when x = 0. So, we can substitute x = 0 into the equation and then solve for the y-value, like so.
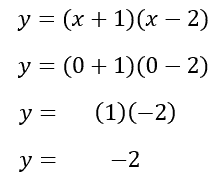
Algebraically, we can see when x = 0, y = -2. Or, (0,-2) is the y-intercept, as its graphs shows to be true.
| ||
The two parabolas below have the same graph.

Why? The reason they have the same graph is because they are mathematically equivalent to each other. The equation on the left side is in factored form, but the equation on the right side is in standard form. If we are asked to change from factored form to standard form, we multiply the factors. To multiply the factors, we can use a multiplication table, like so.
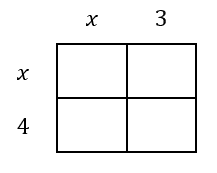
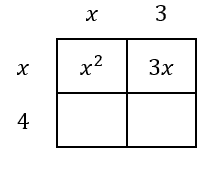
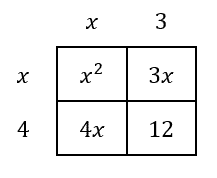
We get these four terms, which will be simplified.
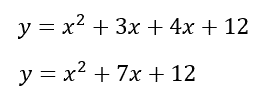
The parabola is now in standard form, not factored form. If you are having trouble following the multiplication process, use the lesson below to review how to multiply polynomials.
One more problem will be shown. This time, the equation in factored form will have a leading number other than one.
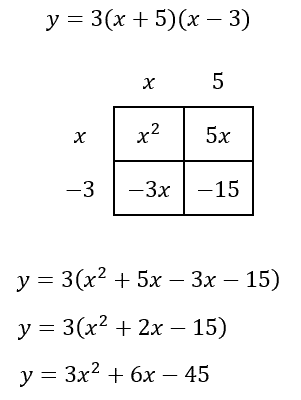
Now you can try a problem of your own by using this MATHguide quizmaster. | ||
Here is a quizmaster related to the lesson above. | ||
| ||
 esson:
esson:  uiz:
uiz: