Parabolas | ||
| ||
Introduction | ||
In this section, you will learn how to graph parabolas. Here is a list of the sections within this webpage:
|
The definition of a parabola is the set of all points that are equidistant to a focal point and a line called a directrix. Howver, it is best recognized by its classic u-shape. Parabolas either open up, down, right, or left. The graphic below will show you how a parabola looks in comparison to its equation.
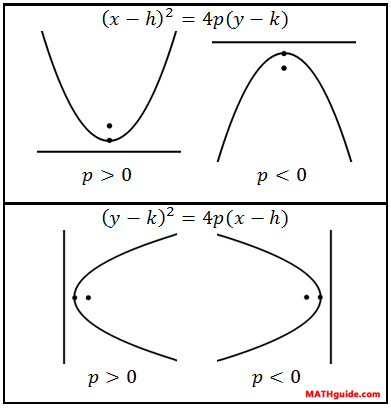
When the x-value is being squared, the parabola opens up when the p-value is positive and down when the p-value is negative. On the other hand, when the y-value is being squared, the parabola opens right when the p-value is positive and left when the p-value is negative. The h-value and the k-value represents the location of the vertex, V(h,k). Therefore, it is important to know the location of the vertex in order to determine the exact equation of a parabola. Conversely, when the equation of a parabola is known, the exact location of the vertex can be determined. Here is a video and a quiz that will help you understand and assess your understanding of parabolas.
| |
ideo: 
uiz: Here are videos related to the lessons above.
|
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
|
Here are activities related to the lessons above.
|
Here related lessons and quizmasters.
|
ctivity: 
esson: