Area of Regular Polygons | ||
| ||
Introduction | ||
In this lesson, you will learn how to calculate the area of a regular polygon. Here is a list of the sections within this webpage:
|
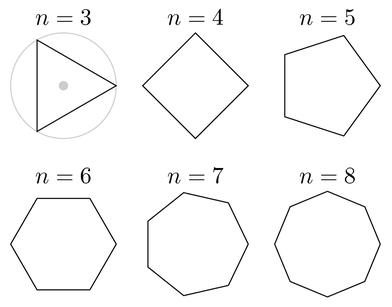
A regular polygon is special type of polygon. It is a polygon that is equilateral (all sides are congruent) and equiangular (all internal angles are congruent). Squares are regular. Rectangles are not because they are not equilateral. Rhombuses are not regular because they are not equiangular. The graphic below shows what regular polygons look like. The letter 'n' stands for the number of sides for each particular polygon: 'n = 3' is a triangle; 'n = 4' is a quadrilateral; ...
| |
There are several steps for calculating the area of a regular polygon. Following these steps requires minimal memorization.
| |
Within the last section, Steps for Calculating the Area of a Regular Polygon, step-by-step instructions were provided for calculating the area of a regular polygon. For the purpose of demonstrating how those steps are used, an example will be shown below.
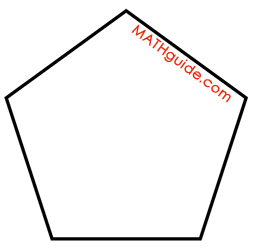
Calculate the area of a regular pentagon that has a radius equal to 8 feet. First of all, we should first sketch a regular pentagon, which has five congruent sides and five congruent internal angles.
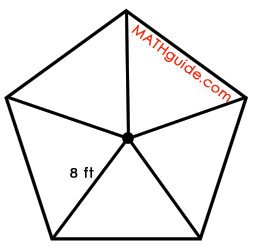
 Step #1: Draw all the radii of the regular polygon. Radii are segments that connect the polygon's center to its vertex, as shown below. Each radius has a length of 8 feet.
 Step #2: Calculate the central angle of the resulting congruent isosceles triangles. As shown in the diagram below, a circle has been drawn so that its center is the center of the polygon.
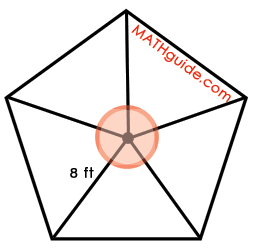 The circle has been divided into five congruent angles by the radii of the polygon. To calculate the measure of one of those central angles, we will recall that a circle contains 360 degrees of angle measure. Since the circle has been divided into five congruent parts, we will divide 360 degrees by five. The result is 72 degrees, as shown in within the next diagram.
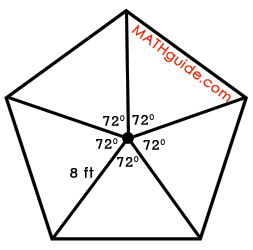 Step #3: Divide the central angles into two parts by bisecting the central angles. In doing so, congruent right triangles will be formed. The isosceles triangles are the five congruent triangles formed by the radii of the polygon. Since the radii are all the same length, each of the triangles have to have two congruent sides, which makes them isosceles triangles by definition. Within the diagram below, one of the isoceles triangles has had its central angle bisected, forming two congruent right triangles.
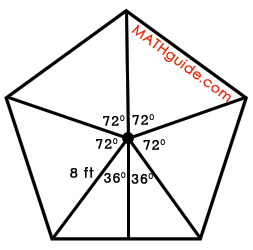 Step #4: Isolate one of the right triangles. Calculate its base length and height using trigonometry. We need to determine the height of the right triangle and the length of its base. As shown in the next diagram, we will label the length of the base with an 'x' and the height with a 'y.'
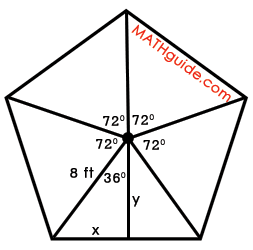 To calculate their values, we will utilize trigonometry. The x-value requires us to use the sine function.
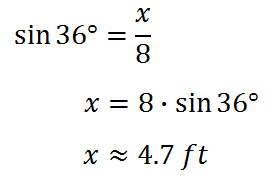 The y-value requires us to use the cosine function.
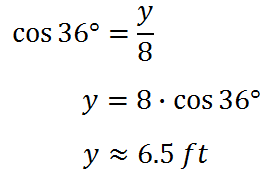 Step #5: Calculate the area of the right triangle by using its base length and height. Now that we know the values for 'x' and for 'y,' those values will be placed in their respective positions, as shown below.
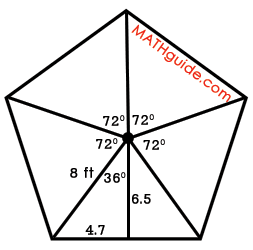 To calculate the area of one right triangle, we will use the correct formula, shown below.
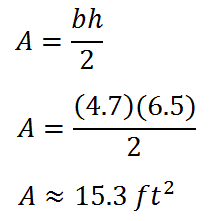 Step #6: Multiply the area of the right triangle by the number of right triangles that were made from the regular polygon. This is the area of the regular polygon. After bisecting all the central angles, it can be seen how many right triangles can be found within the polygon. Use the diagram below to count them.
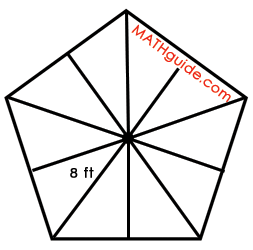 Since there are 10 right triangles and each of them has an area of 15.3, we can multiply 15.3 by ten to get the area of the polygon.
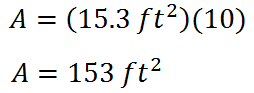 Use the video below to view two examples.
| |
There is a common formula that is used for calculating the area of a regular polygon. This is the formula:
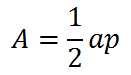 ...where 'a' represents the length of the apothem and 'p' is the perimeter of the polygon. Use the video below to understand how this formula was derived. | |
Here is a video related to the lesson above.
| |
Try this interactive quizmaster.
|
We do not have any activities at this time.
|
Here are related lessons to view.
|
 esson:
esson:  ideo:
ideo:  uiz:
uiz: