Area of Common Figures | ||
| ||
Introduction | ||
There are several sections within this lesson that address common polygons, like triangles, rectangles, and trapezoids, for instance. Use the following sections to learn more about all of these common polygons:
|
A = sum of unit squares | |||
Area is a count of how many unit squares fit inside a figure. To fully understand this classic definition of area, we need to picture the unit square. A unit square is a square that is one unit long by one unit wide. It can be 1'x1', 1 m x 1 m, 1 yd x 1 yd, 1" x 1", ...
| |||
A = lw | |||
A rectangle is an equiangular quadrilateral. Opposite sides are congruent and parallel. All internal angles are right angles.
Let's look at a rectangle that is 4 mm by 6 mm. If we count the number of 1 mm by 1 mm squares that are inside the rectangle we can easily see there are 24 of these squares. After performing the same task with a rectangle that has different dimensions, we can see a pattern.
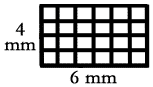 The total number of squares that rest within a rectangle can be found by multiplying the length of a rectangle by its width. So, 4mm x 6mm = 24 mm2, hence the formula A = lw. Counting square units fits nicely with the concept of counting squares and it also coincides with a property of algebra. In algebra, we already know (x)(x) = x2. The same is true for mm times mm, or any unit times the same unit.
Example 1: If l = 20 ft and w = 5 ft, then the area would be... A = lw
Example 2: If l = 11 yds and w = 7 yds, then the area would be... A = lw
| |||
A = bh | |||
A parallelogram is a quadrilateral (four-sided figure) that has opposite sides that are parallel.
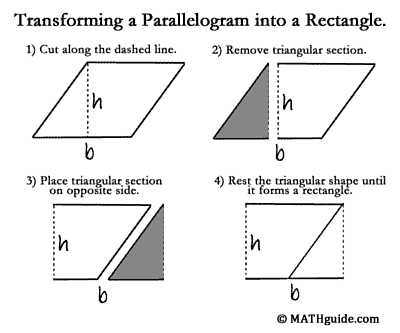
Similar to the rectangle, finding the area of a parallogram requires two known distances. We need to know its height and the length of the side that is perpendicular to the height, called the base of the parallelogram. If we start with a typical parallelogram, we can make a few alterations to it in order to calculate its area. If we cut it along its height, we can remove a portion that is a right triangle. If we move this right triangle to the opposite side of the figure, it will fit perfectly and create a rectangle.
Since we already know the area of a rectangle (see above) to be A = lw, let us apply it to the newly altered parallelogram. The base of the original parallogram is now the length of the rectangle. The height of the parallelogram is now the width of the rectangle. Using the names base and height instead of length and width, we see that the area of a parallogram is A = bh.
Example 1: If b = 7 in and h = 4 in, then the area would be... A = bh
Example 2: If b = 12 m and h = 8 m, then the area would be... A = bh | |||
A = ½bh | |||
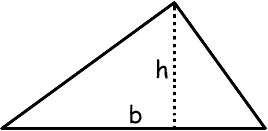
A triangle is a three-sided polygon.
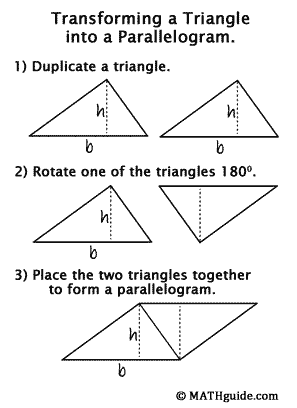
A triangle can be defined by the length of its base and its height. The height is always perpendicular to the base, exactly like the base and height of a parallelogram. We can find the area of a triangle by performing three tasks. First, we duplicate the original triangle. Second, we rotate this duplicate triangle 180 degrees. Third, place the rotated duplicate triangle next to the original triangle so that they fit snuggly together to form a parallelogram.
We know the area of a parallelogram to be A = bh. In our newly formed diagram, we can use those same distances to arrive at the exact same area for the two-triangle area. However, if we want to know the area of one of those triangles instead of the whole parallelogram, we have to divide the area into two equal portions since the triangles are congruent to each other. Therefore, the area of a triangle is A = ½bh.
Example 1: If b = 6 cm and h = 3 cm, then the area would be... A = ½bh
Example 2: If b = 14 mi and h = 5 mi, then the area would be... A = ½bh
| |||
A = ½h(b1 + b2) | |||
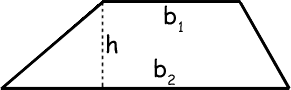
A trapezoid is a quadrilateral that has only one pair of sides that are parallel.
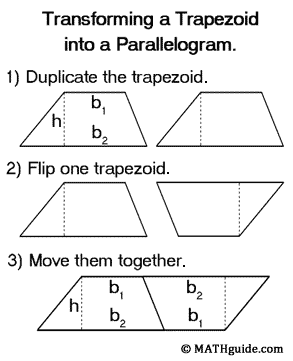
A trapezoid is a quadrilateral with one pair of sides parallel to each other. Let's orientate a trapezoid so that the parallel sides are horizontal and the top side is shorter than the bottom side. Call the length of the top side b1, the bottom side b2, and the height of the figure h. Similar to the process we used with a triangle to find a formula for area, we can 1) create a duplicate trapezoid, 2) rotate the duplicate 180 degrees, and 3) place the duplicate next to the original trapezoid to form a parallelogram. Using some attention to detail, we can see that the base of our newly formed parallelogram is b1 + b2, while the height remains the same as the original trapezoid.
The area of the parallelogram is therefore A = h(b1 + b2). However, since we want to know the area of one trapezoid, we need to divide this amount by two because the two trapezoids that were used to create the parallelogram are congruent to each other. This makes our formula for the area of a trapezoid to be A = ½h(b1 + b2).
Example 1: If b1 = 8 in, b2 = 12 in, and h = 5 in, then the area would be... A = ½h(b1 + b2)
Example 2: If b1 = 9 mm, b2 = 16 mm, and h = 10 mm, then the area would be... A = ½h(b1 + b2)
| |||
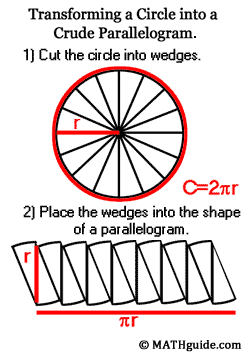
A = πr2 | |||
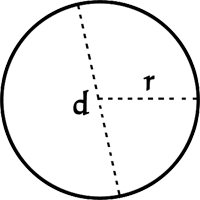
A circle is the locus of all points in a plane that are equidistant from a point.
A circle is a set (locus) of points in a plane that are equidistant from a point. The equidistant amount is known to be the radius of a circle. Even though this simple shape is everywhere around us, is easy to imagine and draw, the formula for calculating the area of a circle is not simple to derive. First, let's start at the center of a circle and cut it into an even number of equally sized pie-shaped wedges. If we arrange these wedges so they lie next to each other such that they alternate pointed up and down and up again until all the wedges are used, the resulting figure will resemble a parallelogram. The more wedges we have, the smaller each wedge will be and a better looking parallelogram will result. The distance around a circle is called the circumference. The distance can be calculated using the formula C = 2πr, where π is the irrational constant approximately equal to 3.14. Since half of the wedges are pointed up and half are pointed down, our parallelogram will have a base equal to half of the circumference. The other base on the opposite side would have a length equal to half the circumference, too. The base, or half the circumference, would be ½C = ½(2πr) = πr. The height of our parallelogram would be the length of our wedge, from the point to the opposite, curved side. This distance is also the radius of the circle. Using the formula for the area of a parallelogram for a base of πr and a height of r would give us: A = bh = (πr)(r) = πr2.
This construction is much harder to perform. Actually, it is impossible to perform with exact precision; however, one can imagine slicing the circle into a number of wedges greater than the number of wedges shown in the diagram above. As the number of wedges increases, a cleaner picture more closely resembling a parallelogram would form. Only when an infinite number of wedges were used could a perfect parallelogram be constructed.
Example 1: If r = 5 ft, then the area would be... A = πr2
Example 2: If r = 9 m, then the area would be... A = πr2
| |||
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
| |||
Discovery lessons can take on various forms and depths. A teacher can use a teacher-directed, Socratic method or a teacher can turn the discovery into a cooperative learning, Montessori exercise. Whether a teacher uses careful direction or provides a few ideas to guide students to the formulas for area, the discovery approach has been shown to be an effective strategy to help students become independant, active learners. As the explanations above for rectangles, parallelograms, triangles, trapezoids, and circles will indicate, the formulas for area of these figures are attainable through discovery. A teacher can guide students to the formulas using critical questions with relative ease. Or, a teacher can explain how duplicating and rotating shapes to create known shapes can make finding area a possibility. Students can then be placed in groups and provide these groups with tools necessary for creating their own figures.
The extent to which students are left discovering these formulas on their own will depend on teacher experience with discovery lessons, student familiarity to discovery exercises, and the maturity levels of students. After students successfully experience the foundations behind the formulas, they will be able to recall these formulas more readily, apply them more accurately, and be able to perform similar experiences when discovering volume of three dimensional solids, which is the next logical sequence for a geometry class.
| |||
This activity reviews the area of several figures within a game format. It also uses ratios.
| |||
After reading the lessons above, try our related lessons.
| |||


 uiz:
uiz: 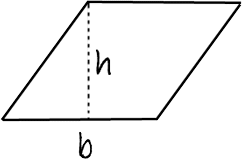
 ctivity:
ctivity:  esson:
esson: