The Point-Slope Formula | ||
| ||
Introduction | ||
In this section, you will learn how to calculate the equation of a line using the point-slope formula. Here are the sections within this lesson:
|
The point-slope formula is to be used when we want to determine the equation of a line. Here is the point-slope formula.
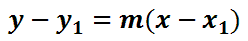
The formula requires a known point, (x1, y1), and the slope, ‘m,’ of a line. The formula is called the point-slope formula because the formula requires both a point and a slope. If we have both of those, then we can calculate the equation of a line.
| |
Let’s say we were given some details concerning a line. If we were told that a line had a slope of 2/3 and a point on the line was (6, 5), we could determine the equation of the line. We will use the point slope formula.
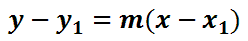
First, we will substitute the point into the equation The x-value is 6 and the y-value is 5.
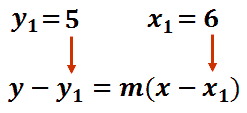
Next, we will place the slope into the equation. The slope is 2/3.
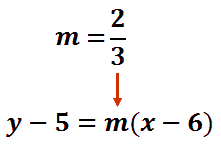
To clean up this equation, let us do the distributive property. We need to multiply everything in the parentheses by 2/3. This will give us.
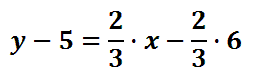
To finish cleaning up, we need to multiply 2/3 times 6, which is 4.
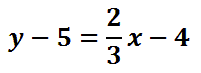
Our last step will be to get the ‘y’ alone, which is called isolating the ‘y.’ To do so, we need to add 5 to both sides of the equation.
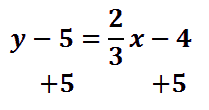
The result is this final equation.
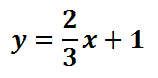
Now, take a look at our video on this topic and test your own skills with a problem of your own.
| |
Let’s say we were given two points on a line, say (-4, -7), and (12, 1), and we wanted to determine the equation of a line. We would have an interesting situation because the point-slope formula requires both a point and a slope. We have a point, but we have no slope. In order to use the point-slope formula, we will first have to calculate the slope of the line. Here is the equation for slope, called ‘m.’
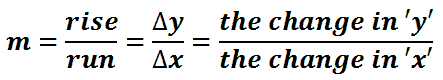
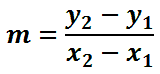
Don’t let the subscripts confuse you. The subscripts, the little numbers at the bottom of the letters, mean the letters are numbered. We are talking about a formula that requires two points. The two points are generically written as (x1, y1) and (x2, y2) for the purposes of the formula. So, we have to decide which of our given points is the first point and which is the second point. It is an arbitrary decision and the answer we be the same regardless. Let us use (-4, -7) as (x1, y1) and (12, 1) as (x2, y2). Let us substitute the values into our slope formula.
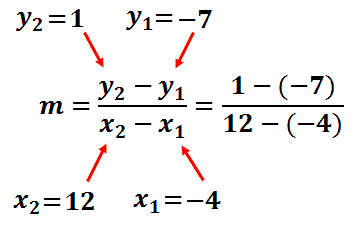
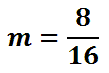
This fraction can be reduced. Left to the reader, the reduced fraction is this.
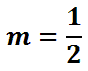
Now that we have a slope, we can use the point slope formula. Our last decision will be which of our two points to use. Do we use (-4, -7) or (12, 1)? Again, it is an arbitrary decision. We can use either point and we will get the same equation of the line. Let’s use (-4, -7) so we can practice using negative numbers. Let’s substitute our point and our slope into the point-slope formula. First, we will insert the slope, 1/2.
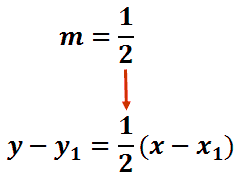
Next, we will place in our point, (-4, -7). Remember, the x-value is -4 and the y-value is -7.
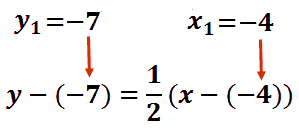
We can cancel the double negatives, because the opposite of a negative number is a positive number.
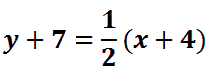
Next, we will do the distributive property and multiply everything in the parentheses by 1/2.
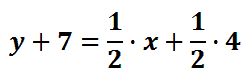
Let’s multiply the 1/2 and the 4. Doing so, we get 2.
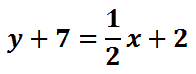
Last, we will subtract 7 from both sides of the equation to isolate the ‘y.’
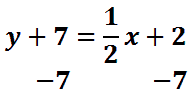
Here is the final equation of the line.
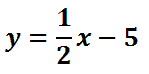
Now, test your own skills with a problem of your own. Use the interactive quiz to try a problem.
| |
Watch our videos that cover the lessons presented above.
| |
Try our interactive quizzes to determine if you understand the lessons above.
| |
Try an activity related to the lessons above.
| |
Try these lessons, which are closely related to the lessons above.
| |
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: