Coordinate Geometry | ||
| ||
Introduction | ||
This page will inform you about coordinate geometry formulas. There are many formulas that involve coordinates, but the following four sections are fundamental to coordinate geometry. Here are the sections within this page.
|
The distance between the coordinates (x1, y1) and (x2,y2) can be obtained by using this formula.
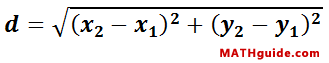
Sometimes this distance is referred to as a length.
| |
The middle of a segment has a special name. It is called the midpoint. The midpoint of a segment separates a segment into two congruent segments that are each half the length of the segment. This is the formula for midpoint given that the endpoints of the segment are at (x1, y1) and (x2,y2).
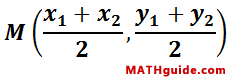
| |
The measure of a line or segment's steepness can be measured. The measurement is called slope and it requires two points, labeled as (x1, y1) and (x2,y2). Here is the formula.
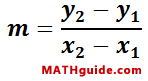
| |
To determine if two lines (or segments) are parallel or perpendicular, this information is necessary to know.
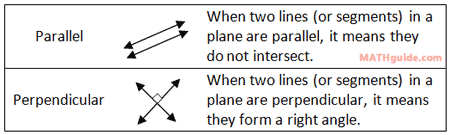
| |
To construct an equation of a line, we can use a special formula called the point-slope formula. The formula requires us to feed it with a point, (x1, y1), and a slope, labeled as an 'm.'
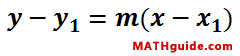
| |
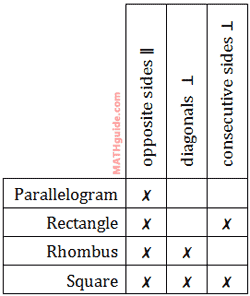
This will test your ability to tell the differences between parallelograms.
| |
Partitioning a segment relies on horizontal and vertical distances.
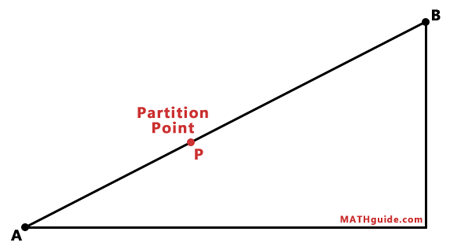
The video below will help you understand how to partition a segment and the quiz will test your understanding of the skills that surround partitioning segments.
| |
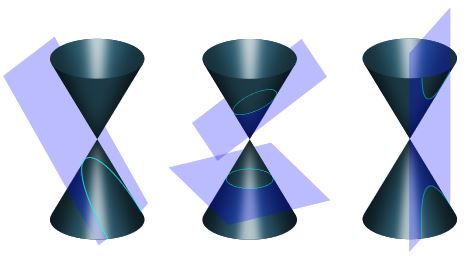
Another area within coordinate geometry rests special shapes, called conic sections. The shapes include parabolas, circles, ellipses, and hyperbolas. See our lesson below. Once there, you will find several lessons, quizzes, and videos.
| |
 ideo:
ideo:  uiz:
uiz:  esson:
esson: