End Behavior | ||
| ||
Introduction | ||
This lesson will teach you how to determine the end behavior of polynomials. Here are the sections within this lesson:
|
For us to determine the end behavior of a polynomial, we first have to know two important characteristics: degree and leading coefficient. The next sections will explain exactly what those characteristics are and how they affect the end behavior of polynomials. If you are not familiar with polynomials, review our lesson before continuing with the rest of this lesson.
| |
Finding the degree of a single variable polynomial is fairly simple. All we have to do is locate the highest exponent. That highest exponent is the degree. For instance, look at the polynomial f(x) = 4x2 - 3x5 + 7 - 2x. Its exponents are 2, 5, 0, and 1. Since the highest exponent is 5, the degree of the polynomial is 5.
If we were examining h(x) = -3x1 + 2x4 + 7x6, we too can find its exponents which have been highlighted in red. The greatest red number is 6, which makes the degree of h(x) equal to 6.
| |
The word 'coefficient' means number in front. However, be careful with this meaning because it refers to the coefficient of the term that contains the highest power. It does not mean the first coefficient that is written. For instance, we saw f(x) = 4x2 - 3x5 + 7 - 2x1 in the last section. The coefficients have been colored blue and the exponents have been colored red. Since the highest exponent is 5, we only look at the term - 3x5 . Since the number in front of the variable is -3, we say that the leading coefficient is equal to -3. When polynomials are written in descending order, the leading coefficient is the first coefficient. Take for instance g(x).
Notice that the exponents start high and then go down in value: 3, 2, 1, 0. Descending order makes it easy to identify the leading term because it will always be the number that leads the polynomial. The leading coefficient of g(x) is -2.
| |
When determining the extreme left and right ends of the graph of a polynomial, begin by looking at the leading coefficient. The sign of the leading coefficient determines if the right branch goes up or it goes down. Here are two facts: a) If the leading coefficient is positive, the right branch goes up.
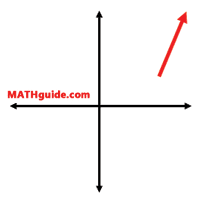
b) If the leading coefficient is negative, the right branch goes down.
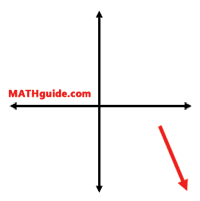
| |
After we determine which direction the right branch points -- either up or down -- we use the degree of the polynomial to help us find out the direction of the left branch. We do this knowing two basic facts: a) If the degree of the polynomial is even, both of the branches go in the same direction.
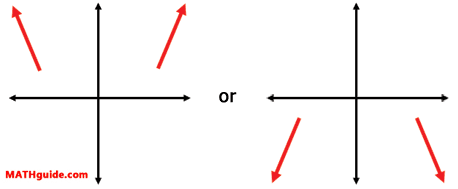
b) If the degree of the polynomial is odd, both of the branches go in opposite directions.
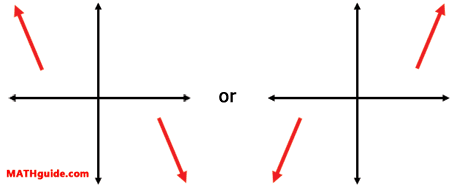
| |
This graphic organizer demonstrates the four cases that exist when considering a polynomial's leading coefficient and degree.
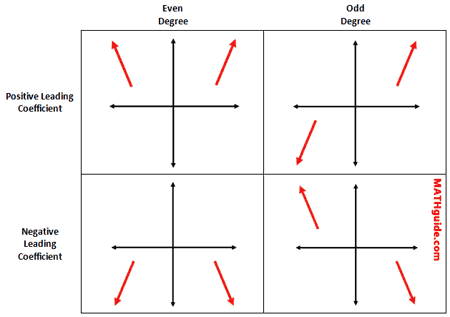
First, look along the left side of the table to view the relationship between the leading coefficient and the right branch.
Second, look along the top of the table to understand the relationship between the degree of a polynomial and whether the end branches go in the same direction or opposite directions.
| |
This video will inform you how to determine the end behavior of polynomials.
| |
Try our interactive quizzes to determine if you understand the material.
| |
Try this lesson, which is closely related to the lessons above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: