Within this MATHguide page, you will learn various characteristics of relations.

• What is a Relation?
• Mapping Relations
• Domain and Range
• Inverses
• Functions
• Polynomials
• Related Lessons

    A relation is a set of ordered pairs. For instance, set S below is a relation.

    S = {(3,2), (2,4), (-6,-2), (-2,1), (0,1)}

    Practically speaking, relations are a comparison from one set to another. For instance, people often look at their earnings over time. We connect the years we have been employed to the earnings we make that year.

    Someone else may be shopping for an above ground pool. That person may want to compare the size of the pool (diameter) to the cost of maintaining it. This would be very useful for someone who is on a tight budget but also wants easy access to a pool.

    Sometimes relations are viewed as a connection of elements from one set to the elements of another set. Using set S from our last section, this diagram will visually indicate what a mapping of sets looks like.

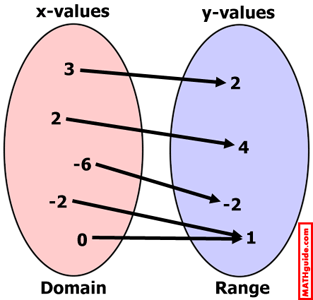
    Notice a few things from the mapping above. It allows us to see that the set of all x-values has a special name, as does the set of all y-values. Also, we can see that two of the x-values map to an identical y-value: referring to (-2,1) and (0,1). This has special meaning and it will be explained in greater detail in the following sections within this page.

    We have a special page dedicated to domain and range. You can access it by using the link below.

    esson: Domain and Range

    Several sections above, we used set S. This is set S.

    S = {(3,2), (2,4), (-6,-2), (-2,1), (0,1)}

To construct the inverse of set S, simply switch the x-values and the y-values, like so.

    S^-1 = {(2,3), (4,2), (-2,-6), (1,-2), (1,0)}

    Notice that the inverse of set S is written as S^-1.

    If we use function notation, the inverse of f(x) is written as f^-1(x).

    We have a special page dedicated to inverses because there is more to the story. You can access this page by using the link below.

    esson: Inverses

    Simply put, a function is a certain type of relation. To learn about functions, use the link below.

    esson: Functions

    Polynomials are special types of functions. To learn about polynomials, use the link below.

    esson: Polynomials

    Try this lesson, which is closely related to the lesson above.

    esson: Domain and Range
    esson: Inverses
    esson: Functions
    esson: Translations
    esson: Testing Relations for Symmetry
    esson: Operations on Polynomials
    esson: Linear Programming