Polynomials, Factors, and Zeros | ||
| ||
Introduction | ||
In this section, you will learn how a polynomial's zeros, factors, and graph are all related. Here are the sections within this lesson:
|
So that you will be able to understand the lessons that follow, we need to review a few definitions.
| |||||||
When polynomials are graphed, many of them intersect the x-axis. The locations where a polynomial crosses the x-axis are called zeros. For instance, we can graph this polynomial.
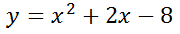
This is the graph of the polynomial.
Notice how the polynomial intersects the x-axis at two locations. It intersects at (-4, 0) and (2, 0). So, we say the polynomial has zeros at -4 and 2.

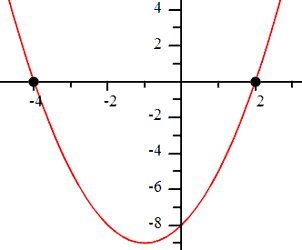
This is the graph of the polynomial.
It can easily be seen that this polynomial has three zeros, namely -1, 0, and 1.
| |||||||
The factors of a polynomial are important to find because they can be multiplied together to gain a polynomial. In our lesson on zeros, we saw this graph.

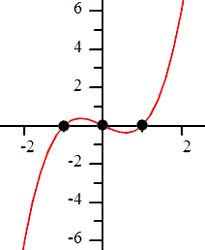
We saw that the zeros were -4 and 2. To get the factors, we simply take the opposite of the zeros. These are the factors.
We also saw this graph in the last section.

It s zeros are -1, 0, and 1. Here are it s factors.
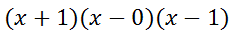
The (x 0) factor is the same thing as writing x. So, here are the factors written more properly.
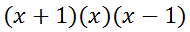
Or, we can write them more compactly as
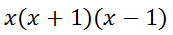
| |||||||
We have an entire section devoted to operations on polynomials, which will come in handy for our next section. You can find it here: Operations on Polynomials. Please review the section before proceeding to the next section.
Besides learning how to add, subtract, multiply and divide polynomials, it is extremely convenient to have a graphing calculator. Modern graphing calculators, like the TI-Nspire CX CAS model, are excellent tools for quickly displaying graphs and consequently speed up the learning process.
| |||||||
We will examine the connection between a polynomial's zeros, factors, and expanded forms. Let's again revisit this polynomial as our first example.
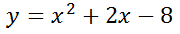
If we look at the graph of this polynomial, we get this picture.

It has the zeros at -4 and 2, which means it has the factors (x + 4) and (x - 2). If we were to multiply the factors (x + 4) and (x - 2), this is what we would get.
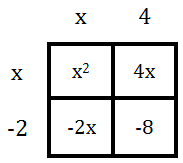
This simplifies as follows.
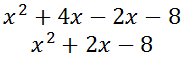
The above polynomial is the original polynomial. This demonstrates how the graph of a polynomial is related to its zeros and its factors.
For our second example, we should look at the cubic polynomial we saw in a previous section.

Viewing this polynomial on a coordinate plane yields this picture below.

It has zeros at -1, 0, and 1, which means its factors are...
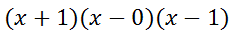
Or, we can write them as...
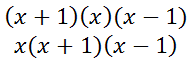
If we multiply the (x + 1) and the (x - 1), we get this.
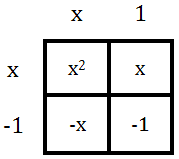
This simplifies as follows.
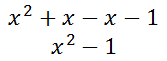
Now, we have to multiply this result by the last factor, x.
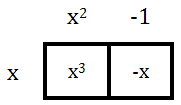
This yields our final result and our original polynomial.

This indicates how a polynomial's expanded form is related to its zeros and its factors. Use this video and quiz to learn more and test your understanding.
| |||||||
This video explains how to use complex zeros to gain factors, and a polynomial expression. It also will inform you of complex conjugate pairs.
| |||||||
When graphing polynomials, there are patterns to follow. These activities and quizzes will assist the learning process to graph polynomial equations.
| |||||||
Like there are logical rules that tell us the connections between zeros and factors, there are also rules that govern the end behavior (branches) of a polynomial. Knowing what the y-values are when the x-values are very large and very small will help us sketch the graphs of polynomials. [Let it be known there is a big difference between even and odd degree and even and odd functions.] This video will instruct you on the connections between a polynomial's degree, leading coefficient, and its end behavior.
| |||||||
When we deal with polynomials, two terms emerge: root and zero. There is a distinction between the two even though some people use them interchangeably. Here are their differences:
The Rational Root Theorem is an involved concept. Understanding it and using requires several layers of explanation, which is done in this video.
| |||||||
Try our instructional videos that detail the lessons above.
| |||||||
Try our interactive quizzes to determine if you understand the lessons above.
| |||||||
Use these activities to learn about polynomials, factors, and zeros.
| |||||||
Try these lessons, which are closely related to the lessons above.
| |||||||
 uiz:
uiz:  ideo:
ideo:  ctivity:
ctivity:  esson:
esson: