Rational Expressions with Exponents | ||
| ||
Introduction | ||
In this section, you will learn a variety of properties and applications involving logarithms. Here are the sections within this lesson:
|
An exponent is a little number written to the upper right of a number or mathematical expression. The value 'two' below is an exponent, which is sometimes called a power.'
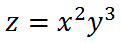
The 'three' above is also an exponent.
| |||||
Exponents are shorthand for multiplication. It indicates how many times an expression or value should be multiplied by itself. To better understand this, we need to look at an example. If we substitute x = 3 and y = -5 into our formula above, this is what we will get.
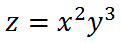
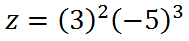
Now, we will write out all the factors so we can calculate a product.
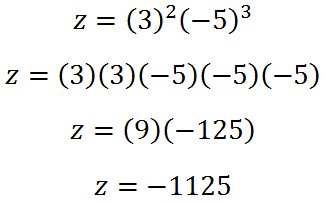
Exponents hold for expressions, too. We should examine another expression, like this one.
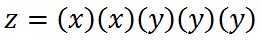
Since we are multiplying two x-variables together, we can simplify it using exponents.
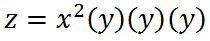
We can do the same for the y-variable.
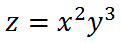
This means the expression above means we are multiplying two factors of 'x' and three factors of 'y.'
| |||||
There are a few properties of exponents that we will need for the following sections. We need to look at a few examples, first.
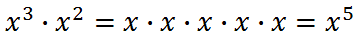
It's clear that we should add powers when we multiply like bases. Let's look at what happens when we divide like bases.
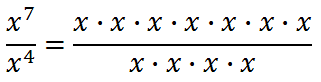
In this situation, we can cancel terms.
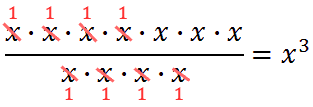
Here are the properties in abstract form.
There is one more property. We need to look at a situation that involves compounded exponents, like this one.
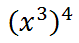
The fourth power means there are four factors to multiply.
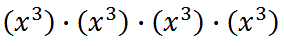
Now, we need to use property one to clean this up.
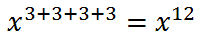
It is evident that there is a shortcut for this situation. When raising an expression to an exponent that already contains an exponent, we can multiply exponents.
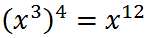
This takes us to our third property.
There is a situation that we should explore that involves property two. Let us look at this example.
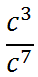
We need to subtract the exponents.
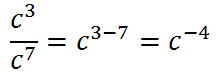
We have to determine what this negative exponent means. If we back up and review the simplification of the problem, it will be easier to do so.
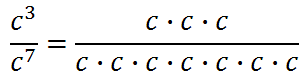
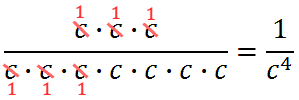
The negative exponent simply means there are that many factors in the denominator. This leads us to this property.
The above properties will be inferred within the sections below. However, use the link below to watch an instructional video that will explain how the rules work.
If you would like to read about a detailed look at properties of exponents, see our lesson called Power Rules of Exponents.
| |||||
We need to look at a few examples of expressions involving exponents. Example 1
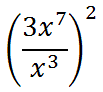
To start, we will use property two and subtract the exponents inside the parentheses.
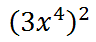
Next, we will write two factors because of the square on the outside of the parentheses.
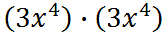
Multiplying the factors, we will use property one and get this.
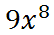
Example 2
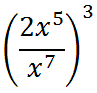
We will start with property two and subtract exponents.
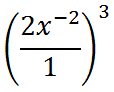
We learned that the negative exponent simply tells us there is a factor of 'x' in the denominator (property four), like this.

Next, we will write three factors, due to the exponent outside the parentheses.
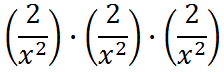
Multiplying the factors and using property one gives us this.
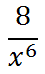
Example 3
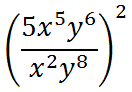
We will start with property two and subtract exponents from like bases.
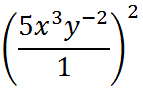
Next, we will use property four and move the factors of 'y' to the denominator.
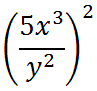
We now need to write two factors, due to the square on the outside of the parentheses.
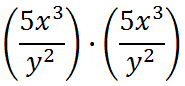
Last, we are going to use the first property and add exponents from like bases.
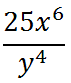
This is the final answer. Try the instructional videos and quizzes below to continue learning and testing your knowledge of rational expressions involving exponents.
| |||||
It is now time to look at examples that are more complicated. This next section involves problems that have negative exponents. Example 1
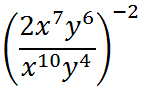
First, we should realize that the value two does have its own exponent. like so.
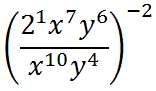
Now, we can use property two.
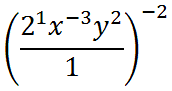
Now, we will use property four.
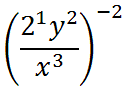
Let us now use property three.

Next, use property four, again.

Last, we can square the '2.'
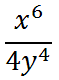
Example 2
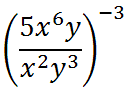
First, we should realize that the value '5' does have its own exponent, as does the 'y,' like so.
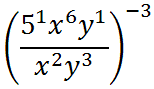
Now, we can use property two.
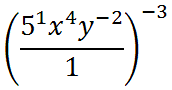
Now, we will use property four.
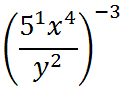
Let us now use property three.
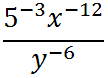
Next, use property four, again.
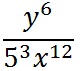
Last, we can cube the '5.'
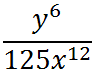
 ideo: Rational Expressions Involving Exponents: Negative Exponents ideo: Rational Expressions Involving Exponents: Negative Exponents
| |||||
Try our instructional videos to determine if you understand the lessons above.
| |||||
Try our interactive quizzes to determine if you understand the lessons above.
| |||||
There are no activities posted yet. Come back soon to find some. | |||||
We would like to invite you to learn from our other advanced trigonometry lesson.
| |||||
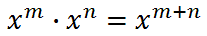
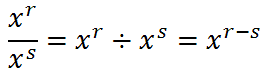
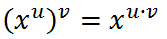
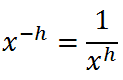
 uiz:
uiz:  esson:
esson: