Limits: Numerical Approach | ||
| ||
Introduction | ||
This lesson page will inform you how to find various limits of piecewise functions. Here are the sections within this page:
|
In a nutshell, the act of pursuing a limit is to get closer and closer to an x-value of a function while observing the y-values to determine if there is a trend. If we approach the x-value from the left get a certain y-value value and approach the same x-value from the right and get an equal y-value, we say the function has a limit. Only when the two trends match do we say there is a limit and assign it to that y-value trend. For instance, if we wanted to find the limit...
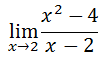
...we would have to approach the x-value 2 from the left and the right. To approach the x-value 2 from the left, we could use this table.
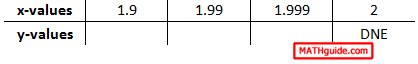
Notice these two points:
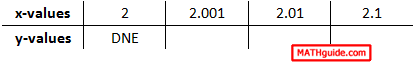
Starting with the x-value 2.1 and working left, we can see that the x-values are getting closer and closer to the x-value 2.
By evaluating the expression at each of those values in both tables, we can determine what the trend is for the y-values. We will continue this process within the next section.
| |
Within the last section (see Pursuing Limits) we began a process for viewing a trend in y-values as we approached a certain x-value, which was 2. This section is labeled as 'Difficult Cases' because the limit at the x-value 2 is not easy to find by simply evaluating the function at the x-value 2. This is so because the function is undefined at the x-value 2. This is why we are using this numerical approach. Here is the problem we were working on the last section.
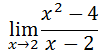
Continuing with our numerical approach from the last section, we will fill in the rest of the tables. To do so, we need to plug in x-values within the function. Leaving the calculation to the reader, we gain these values for the finding the limit as we approach the x-value 2 from the left.
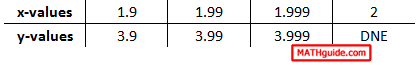
Here is the other table, which approaches the x-value 2 from the right.
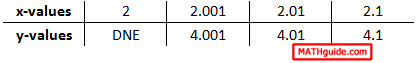
When we place these two tables together, the trend is the same regardless if we approach the x-value 2 from the left or from the right.
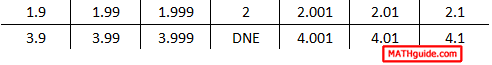
If we ignore the DNE, we can clearly see that the y-values approach the same value whether we move from the left side or from the right side.
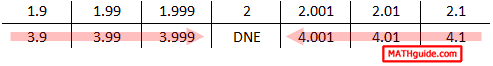
The trend for the y-values is that they approach the value 4 as we get closer to the x-value 2. Hence, 4 is the limit. Here is the original problem with its appropriate solution.
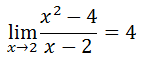
| |
Let us examine this limit.
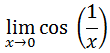
This is another tough case. One reason is that it cannot be evaluated at the x-value 0. The other reason is because it is a peculiar function with a reciprocal argument within the cosine function. However, this limit can be calculated numerically with little problem. We have to create a table of values and then determine if a trend exists and what that trend is if it does exist. Here is the table with x-values filled in.
Our next step requires us to plug in those x-values into the function to determine their respective y-values. We already know the y-value when the x-value is 0; it is undefined. Yet, here is the complete table. Note: this table is the result of calculating within radians.
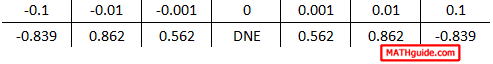
As we look at this table, we certainly see symmetry. The values on the right are mirror values of those on the left, but no numerical trend can be seen. If we carry our precision to even greater detail, we get this table of values.
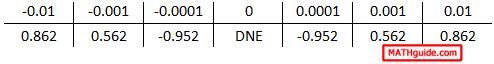
It becomes even clearer that even though there is symmetry within the table and that it is predictable in that regard, but no trend exists as we move closer to 0. The y-values fluctuate without headed toward any particular value. Therefore, the limit does not exist. We write the solution like so:
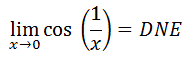
| |
When dealing with limits of functions when we approach negative x-values, it is extremely common to create tables of values that have errors. For instance, if we wanted to evaluate this limit...
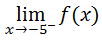
...we would have to approach the x-value -5 from the left. We would set up our table like so.

Placing the -5 on the right side of the table is necessary because we need to approach -5 from the left. As we get closer to -5, we can start with -5.1, which is to the left of -5.
Next, we have to continue filling in values -- getting closer to -5.
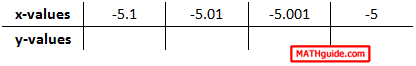
Typically, people get these values wrong for several reasons (but will not be discussed here). Let us also gather a table for this limit, which is the other side (right side) of the x-value -5.
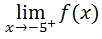
Here is the table for this limit.
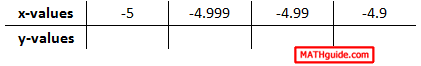
The words of caution are to be extremely careful when crafting the x-values for these tables when dealing with negative x-values. If we place the left limit table and the right limit table together, we get this table.
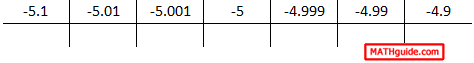
Be mindful of number order and precision. Knowledge of these two characteristics will help you create accurate tables for numerical analysis when calculating limits.
| |
Try this instructional video to learn this lesson. | |
Try this interactive quizmaster to determine if you understand the lesson. | |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: