Functions | ||
| ||
Introduction | ||
In this section, you will learn how to model the flight of a projectile using a polynomial function. Here are the sections within this lesson:
|
When we write mathematical expressions, we can graph those expressions. They are all called relations. However, some of them are special and we call them ‘functions.’ The best way to be able to distinguish these special relations called functions is to use something called the ‘vertical line test.’ Graph the relation. Imagine moving a vertical line throughout the graph. Look to see how many times a vertical line can intersect the relation. If the maximum number of intersections is one, then the relation is a function. Here are some examples using letters of the alphabet. The vertical line is in red and the points of intersection are green. The four words are ‘MATH,’ ‘VERY,’ ‘COOL,’ and ‘WILD.’ Can you spot the two letters that pass the vertical line test?
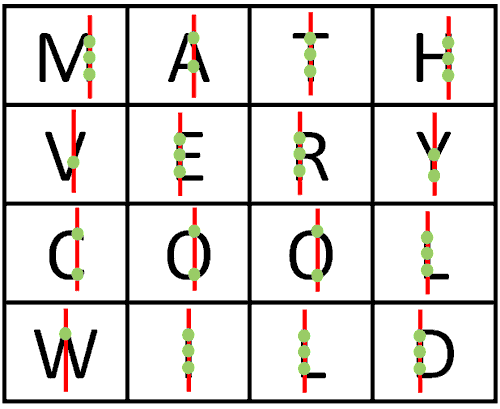
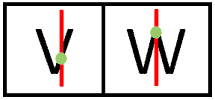
The ‘M’ fails the vertical line test because a vertical line passes through the right and left sides a countless number of times. The same is true for the ‘D,’ ‘L,’ ‘E,’ ‘H,’ ‘T,’ ‘I,’ ‘R’ and the ‘Y.’ The ‘A,’ ‘C,’ and the ‘Os’ intersect twice with a vertical line, which also disqualifies them from being classified as functions. If you said ‘V’ and ‘W’ pass the vertical line test, then you are right! A vertical line intersects with them only once, making them functions.
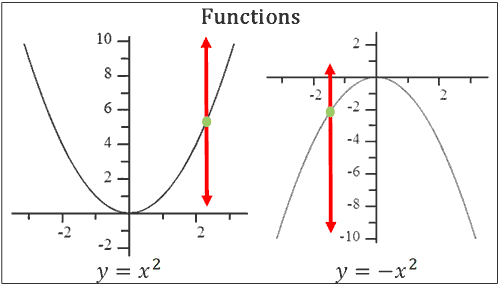
Likewise, parabolas that face upward and downward are functions, too (see below). They are functions because a vertical line intersects the curve no more than once.
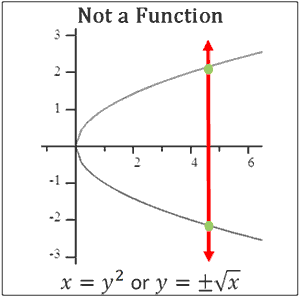
However, the parabola that opens sideways is not a function. Notice how a vertical line intersects the sideways parabola twice (below), thereby disqualifying it as a function.
Try our quizmaster to determine if you know how to tell the difference between a function and a non-function. | |
As we saw from the previous section, functions are special relations. They are used for a variety of tasks, like calculating areas, volumes, tax amounts, and profit margins for companies to name a few. Here are two functions. One is called f(x) and the other g(x).

The letter is the name of the function and the "x" next to the name stands for the variable used within the formula. Some people mistake the f(x) to mean 'f' times 'x,' but the 'x' simply tells us which letter is the variable in the function.
| |
When we evaluate functions, we replace the variable with values. If we use f(x) from the section above, we can evaluate the function when the x-value is -3. We write the problem like this: "Evaluate f(-3)." To do so, we substitute the x-value with -3, like so.
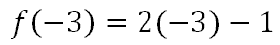
Now, we let the order of operations tell us how to proceed. We multiply first.
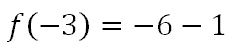
Finally, we subtract.
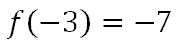
Try our quizmaster on this topic by using the link below.
We should look at a real problem involving functions. If we wanted to know what the Celsius temperature was when the Fahrenheit temperature was 104°, we would need to use this function, where 'x' stands for the Fahrenheit temperature and the 't' stands for the Celsius temperature.
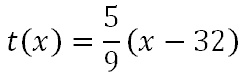
To indicate we want to evaluate the function with the value 104, we write this:
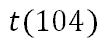
This means we want to replace the variable, the 'x,' with 104. Consequently, the evaluation process looks like this.
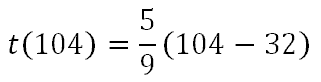
Notice that the 'x' was replaced with 104. Now, we will use the order of operations to evaluate. We will first do the subtraction, because it is within parentheses.
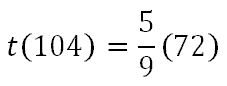
Next, we divide 72 by 9.
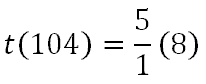
Last, we multiply 5 and 8.
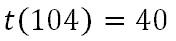
This means 104 degrees Fahrenheit is the same temperature as 40 degrees Celsius. Try our quizmaster on this topic by using the link below.
Here is another example. Say one wanted to know the area of a square. The formula can be represented with this function, where 'x' represents the length of one side of a square and 'A' is the area of the square.
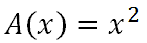
If we wanted to calculate the area of a square that has a side length of 9 feet, we evaluate like so.
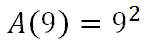
Now, we do what the formula says to do and we square the '9.'
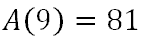
The area of this square is 81 square feet. Try our quizmaster on this topic by using the link below.
| |
Sometimes it is necessary to calculate the following three problems:
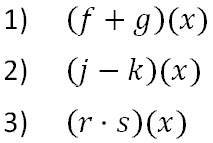
This notation directs us on what to do with the functions f(x), g(x), j(x), k(x), r(x), and s(x). For the problems above, we will use these functions.
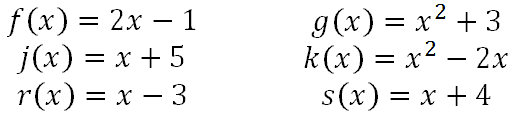
Before proceeding, if you need a refresher on how to add, subtract, and multiply polynomials, review our lesson on polynomial operations. Problem 1: (f + g)(x) This problem indicates f(x) and g(x) are to be added together, like so.
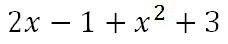
Adding like terms, we get this solution.
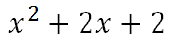
Problem 2: (j - k)(x) This problem indicates that k(x) must be subtracted from j(x), like so.
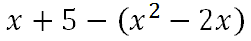
We have to change this problem to addition by taking the opposite of the second function.
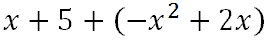
Now, combine like terms to get the solution.
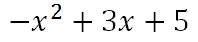
Problem 3: (r • s)(x) This problem requires us to multiply the two functions, like so.
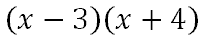
Some people use a table to do this multiplication. The steps on how to complete the table are not shown here, but detailed steps are shown within our operations on polynomials lesson. Here is the completed table.
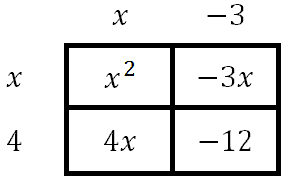
Here are the four terms.
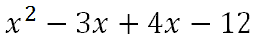
Combining like terms, we get this solution.
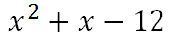
| |
A composition of functions is very similar to our evaluation of functions explained in the section above on evaluating functions. However, it requires a greater amount of algebra to understand. For instance, let us examine two different problems, but we will use these functions for both problems.

Problem 1: Evaluate (f ο g)(x) This open circle symbol means this.
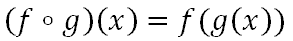
Instead of placing a numerical value inside the f-function, instead we are required to place the entire g-function in for 'x.' Recall, if we calculate f(5), it means we replace the 'x' with 5 inside the f-function. It would mean we would take our value of five, multiply it by 2, and subtract 1. Similarly, we will replace the 'x' with g(x), carefully, as shown here within the f-function.
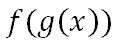
We will include g(x) within this problem.
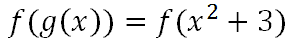
Now, we will replace the 'x' in the f-function with the x-squared plus 3, like so.
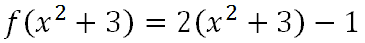
Next, we will let the order of operations tell us to do the distributive property and multiply the terms in the parentheses by two.
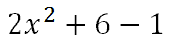
Last, we will combine like terms.
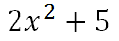
Problem 2: Evaluate (g ο f)(x) This problem turns out to be substantially different from example 1, even though it uses the same functions, f(x) and g(x). However, now we are placing the f-function inside the g-function.
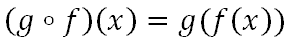
If we were to evaluate g(7), we would replace the 'x' with 7 inside the g-function. We would have to take the seven, square it, and add 3. Likewise, we will do the same thing with the f-function. We will square it and add 3 to get the final answer. Here are the steps.
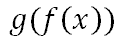
We will introduce the f(x) to the problem.
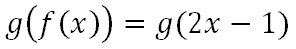
Next, we will replace the 'x' with f(x), like so.
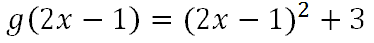
Although all the details are not shown, a table was used to square the binomial to get this.
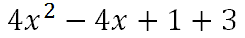
Now, we will add like terms to get the final answer.
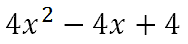
| |
Now that you have some experience working with functions, it is time to test your ability to find patterns with linear functions. Use this interactive quiz to see if you can take a table of values and construct a linear function that matches it. | |
This next interactive quiz is much like the Determine the Function quiz from the last section. However, the table of values found within this quiz use two independent variables instead of one, which makes it a more challenging test of ability.
We also have a related interactive game. Try it to see if you have pattern recognition skills.
| |
View our instructional video on parent functions.
Also, try these interactive quizzes to determine if you understand the lesson.
| |
View our instructional videos related to functions.
| |
Try our interactive quizzes to determine if you understand the lessons above.
| |
Use these activities to help you learn functions and solidify their properties.
| |
Try these lessons, which are closely related to the lesson above.
| |
 uiz:
uiz:  ideo:
ideo:  ame:
ame:  ctivity:
ctivity:  esson:
esson: