Unit Vectors | ||
| ||
Introduction | ||
In this lesson, you will learn how to create a unit vector. Here are the sections within this page.
|
A unit vector is any vector that has a magnitude equal to one. Magnitude is a word that means length of a vector. So, any vector that has a length equal to one is a unit vector.
Symbolically, it is written like this: |v| means the magnitude of v. So, if |v| = 1, then v is a unit vector.
| |
We have seen unit vectors in our section called Engineering Notation. We saw that there are standard unit vectors called i, j, and k. Technically, engineers place a mark over the letters and call then i-hat, j-hat, and k-hat, respectively. For instance, i-hat is a vector of length one that heads to the right on a Cartesian plane. I-hat is written as...
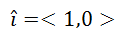
Read more about these orthogonal vectors in our Engineering Notation section.
| |
A unit vector calculation is accomplished by taking a non-zero vector and dividing it by its magnitude, as described here.
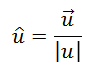
Just like i-hat is a unit vector, u-hat is the symbolic representation of a unit vector. The arrow sign above a letter indicates it is a vector. the hat sign above a letter indicates it is a unit vector.
| |
Use these examples to learn more about the calculation process. Example 1: Find a unit vector in the direction of w = <-4,2>. The first calculation is to determine the magnitude of <-4,2>, which is its length. For that we could first sketch the vector, like so.
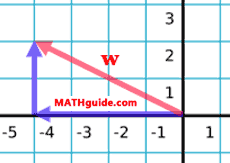
The magnitude is the length of the vector or the hypotenuse shown in the diagram above. Using the Pythagorean Theorem, we get this.
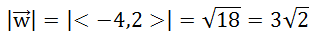
Now all we need to do is to divide the components of the vector by its magnitude to get the unit vector. This is written mathematically like so.
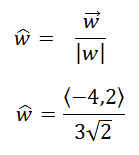
We will divide the components accordingly.
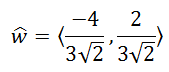
Using a calculator, we get this decimal version, rounded to the nearest hundredth.
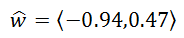
Example 2: Find a unit vector in the direction of v = <3,-4>. For this example, less work will be shown. Nevertheless, let us first determine the length of the vector. The Pythagorean Theorem, yields this.
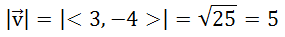
Since the magnitude of the vector is equal to 5, we need to divide the components by 5. Here is the final answer.
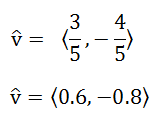
 uiz: Unit Vectors uiz: Unit Vectors
| |
Try this instructional video on unit vectors.
| |
Try these quizzes to see if you understand the content above.
| |
Try these lessons, which contain more information on vectors.
| |
 esson:
esson:  ideo:
ideo: