Properties of Rectangles | ||
| ||
Introduction | ||
This lesson page will inform you about the properties of rectangles. Here are the sections within this lesson page:
Before reading on with the sections in this lesson, we recommend that you first review this lesson:
|
A rectangle is an equiangular parallelogram. Since a rectangle is a parallelogram and a parallelogram is a quadrilateral, a rectangle has all of the properties of both a parallelogram and a quadrilateral in addition to being equiangular.
The sections below will address the properties that are unique to rectangles.
| |
If the internal angles are equiangular, they are congruent (by definition of equiangular). We know that the internal angles of a quadrilateral have a sum of 360 degrees (see Properties of Quadrilaterals, Property: Internal Angles). Since the angles are congruent, they must all be equal to 90 degrees.

Four Right Angles | |
Here is rectangle ABCD with diagonals AC and BD.
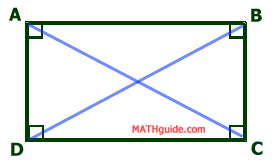
There are numerous triangle in the diagram. However, we will focus on two overlapping triangles, triangles ADC and BCD. Opposite sides are congruent for parallelograms; so, segment AD is congruent segment BC. Segment DC is congruent to itself by the reflexive property. In the last section (Properties: Internal Angles), we found that all the angles are 90 degrees. If we pull out the triangles from the diagrams and their congruent attributes, this is what we see.
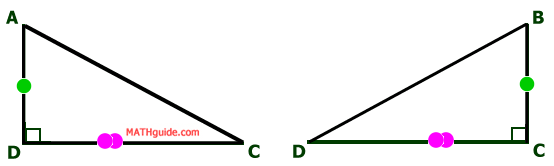
Triangle ADC is congruent to triangle BCD by SAS. By CPCTC, segment AC is congruent to segment BD. This means...
Rectangle are Congruent | |
Review these related lessons
| |
 esson:
esson: