Standard Deviation | ||
| ||
Introduction | ||
This lesson page will teach you about standard deviation. Here are the sections within this lesson page:
|
 Collecting data and analyzing it is how we come to understand situations.
Collecting data and analyzing it is how we come to understand situations.
Nurses collect height, weight, pulse, temperature, and blood pressure to help measure a patient's health. Quality control specialists examine various attributes of items from an assembly line (like dimensions, color, texture, or taste if dealing with food) to determine if the items are being manufactured correctly. Teachers review classroom participation, assignment completion, and quiz and test scores to see if students are learning. Schools look over a variety of data, too, like student behavior, graduation rates, and attendance and search for patterns.
We will see how calculating and utilizing standard deviation helps us to understand the data we collect to determine if it is extreme or not.
| |||||
There are two formulas to calculate standard deviation. If we have all the data in a set, we use this formula:
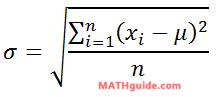
...where 'xi' is each value in our set and 'μ' is the mean of the set. If we have a sample of the data in a set, we use this formula:
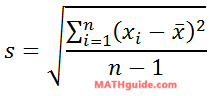
...where 's' is the sample standard deviation and 'x-bar' is the sample mean.
| |||||
If we are given a set of data, we have to first calculate its mean. Let us use this sample data for the purpose of calculating mean and then the sample standard deviation.

From our knowledge of Frequency Tables, we know this data can be written as a set of data, like so.
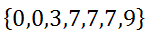
The mean is simple to calculate. Here it is shown:
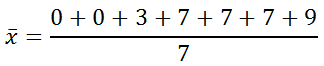
Adding the numerator and cleaning up, we get this:
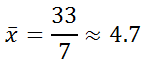
Now, we have to subtract the mean from each value in our set, like so.
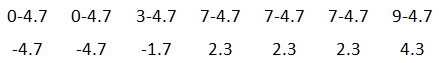
Our next step is to square these differences.
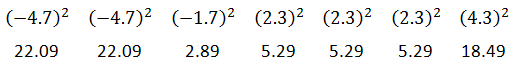
The sigma in the formula means to add the numbers. So, here is the sum.
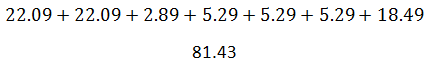
The formula tells us to divide this sum by one less than the number of data values we have. We have seven data values; so, we will divide by six.
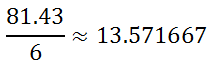
The last step demands that we take the square root.
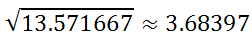
If we round this to the nearest hundredth, we get...
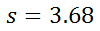
| |||||
It is absolutely true that no one uses formulas when calculating standard deviation. Instead, either an advanced calculator or a software product is used. Graphing calculators have a built in method for calculating standard deviation and sample deviation. This is true for other calculator manufacturers, which includes Casio and Hewlett Packard. However, the explanation below will use screenshots and explanations using the TI-Nspire calculator. Let us get started by using the same data presented in the last section. We have.

To begin, we have to get a new document. So, we have to press the home button to get a new document.
Then, we select "Lists and Spreadsheet."
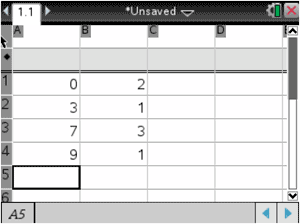
Next, we plug in the data we have in the same two-column format.
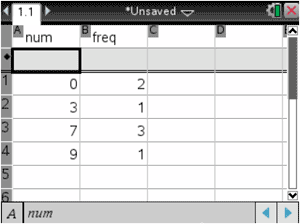
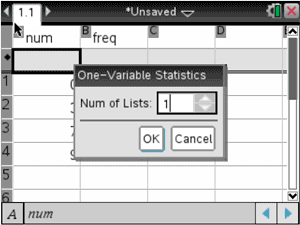
It is recommended (but optional) that we label the columns. Here, the top of column 'a' is labeled 'num' and the top of column 'b' is labeled 'freq.'
Now, we want the calculator to determine the mean and sample standard deviation. We press Menu, then Statistics and Stat Calculations, as shown here:
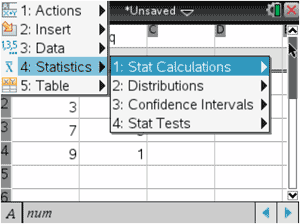
Then, select One-Variable Statistics, like so.
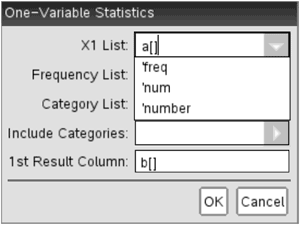
We now have to set the next menu. The 'x1 list' is asking for the column that contains the numbers in our data set. We can leave it as a[] to indicate column 'a' or we can click on 'num' from the dropdown menu, as shown here:
Next, click on the dropdown menu from the line marked 'Frequency List' to select either 'freq' or we can type in b[] to indicate column 'b.'
In the line marked '1st Result Column,' we have to indicate where we want the data printed. Since columns 'a' and 'b' are already occupied, make sure to type in c[] to indicate column 'c.' Here is a screenshot.
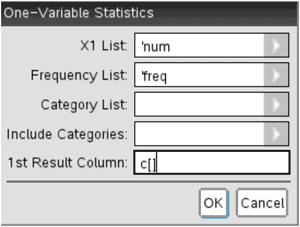
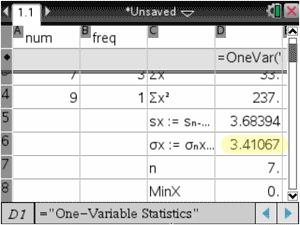
This next screen contains what we were looking for, namely the mean (labeled as x-bar) and the sample standard deviation (labeled sx), which has been highlighted below.
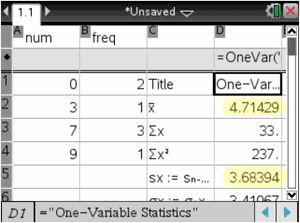
If we had all the data in the set and we were looking for the standard deviation (not the sample standard deviation), we would use the σx-value instead, which is highlighted in this menu.
| |||||
Standard deviation measures how much spread there is to a data set. If a data set has a high standard deviation, the data spreads far to the left-right. If a data set has a small standard deviation, the data is more horizontally compact. This can be best demonstrated by comparing two data sets that have different standard deviations.
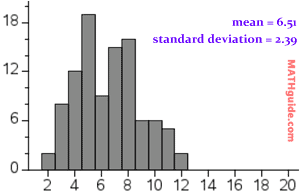
The histogram below is the result of rolling two 6-sided dice 100 times and recording the sum of the two dice. [See our Dice Roller: Mean, Standard Deviation interactive quizmaster to roll your own dice]. The mean is 6.51 and the standard deviation is 2.39.
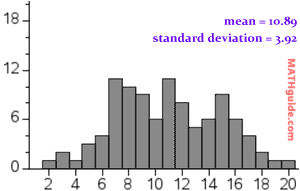
The histogram below is similar to the situation above, but instead two 10-sided dice were rolled 100 times and the sum of the dice was recorded. [The Dice Roller: Mean, Standard Deviation was used again.] The mean is 10.89 and the standard deviation is 3.92.
The scales are both set to the same values to make the comparison possible. Notice that the graph with a higher standard deviation is wider than the graph with the lower standard deviation. This is evidence to support the claim that standard deviation informs us of the amount of horizontal spread in the data.
Also, numbers that are far away from the mean of a data set are numbers that become more rare. Look at the next section to see how plotting mean and standard deviation on a number line can be used to describe common values versus uncommon values in a data set.
| |||||
This section will teach you how to use a horizontal graph with mean and standard deviation to determine the rarity of numbers within a set. Example 1: It has been said male heights have a mean of 69.1 inches and the standard deviation is 2.9. Plot this information linearly in a horizontal format. The line graph below has the mean in the middle (marked with a red line segment). The number to the right of the mean is one standard deviation greater than the mean or 69.1 + 2.9 = 72. Similarly, the number to the left of the mean is one standard deviation lower than the mean or 69.1 - 2.9 = 66.2.

We can keep adding standard deviations (+2.9) as we move to the right and subtract standard deviations as we move to the left (-2.9). The horizontal graph below shows one more standard deviation right and left.

With the horizontal graph below, one more standard deviation right and left is shown.

Numbers that are several standard deviations from the mean are rare occurrences. For instance, being 6 feet tall (72 inches or one standard deviation to the right of the mean) is not uncommon. However, males who are more than two standard deviations to the right of the mean is uncommon. In fact, about 2.5% of the male population has a height greater than two standard deviations from the mean. Heights three or more standard deviations to the right is rarer still. Less than 1% of the male population is that tall! Example 2: If a soda machine dispenses large sodas with a mean of 12 ounces and a standard deviation of 0.07 ounces, create a horizontal graph that includes three standard deviations. In general, we must place the mean at the center of the line graph (because the mean represents the center of the data) and we keep adding standard deviations to the right. We keep subtracting standard deviations to the left. So, in general the graph should look like this:

To address the soda machine, we will place 12 at the center. To the right, we must place three standard deviations. This is what the math looks like.
12 + 1(0.07) = 12.07 To the left of the mean, we subtract standard deviations, like so.
12 - 1(0.07) = 11.93 With all the numbers in place, this is our line graph to three standard deviations.

| |||||
Try this quiz, which can help you learn the content above. | |||||
Try this lesson and quizmaster, which are related to the sections above.
| |||||
 uiz:
uiz:  esson:
esson: