Volumes and Lengths of Similar Solids | ||
| ||
Introduction | ||
This lesson will allow you to understand the relationship between Volume and corresponding lengths of similar solids. Here are the sections within this lesson page:
If you are not familiar with ratios, similarity, and proportions, it is strongly suggested that you first review these lessons before proceeding.
|
If a cube with sides of unit 1 were to be doubled in length, width, and height, would the resulting cube be twice the volume as the original cube? Here is a cube. Each edge has a length equal to 1 unit.

If we double all of its dimensions, we would gain a larger cube. Each edge would have a length equal to 2 units, like this cube.

Now, we need to determine their volumes to compare them. Remember, volume is a measure of unit cubes that a solid occupies. The small cube is a single cube. It has a volume equal to 1 u3. The larger cube has four cubes on top and four cubes on the bottom. That is a total of eight cubes or 8 u3. Let us examine their volumes side-by-side in this table.

We can see that the larger volume is not double the volume of the small cube. The larger cube is 8 times the volume of the smaller cube. Doubling the length of a cube does not double the volume.
The next section will provide a detailed mathematical relation between ratios of lengths and ratios of volumes between similar solids.
| |
The relationship between lengths and volumes is not a 1:1 relationship between similar solids. This fact was demonstrated in the previous section (see Question). This equation describes the mathematical relationship between the lengths and volumes of two similar solids.
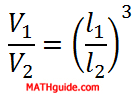
The mathematics tells us that the cube of the ratio of the lengths is equal to the ratio of the volumes.
The next two sections will show you how to use the relationship, much like a similar relationship was used for areas of similar figures (see Areas and Lengths of Similar Figures).
| |
We will look at a situation that asks us to work with similar solids. Example: Determine the volume of the larger of these two similar solids using the information provided within the diagram below.
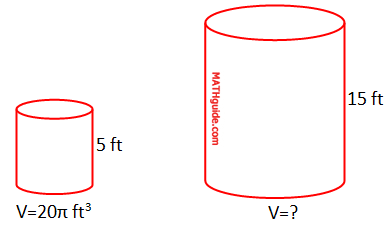
This problem hands us a volume of the smaller solid. It also gives us the heights of the two solids, which are corresponding lengths between two similar solids. So, we can use the relationship described in the previous section (see Relationship Between Lengths and Volumes).
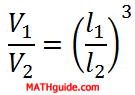
We can substitute the smaller volume in the numerator. Likewise, we need to put the smaller height in the numerator of the second fraction, like so.
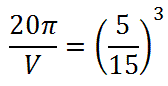
Before cubing the fraction, it would be wise to first reduce it. We can divide by a common factor of 5 and then cube the fraction.
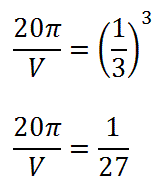
Next, cross-multiply (see Proportions).
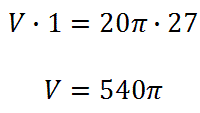
This means the larger cylinder has a volume equal to 540π ft3 or approximately 1696.5 ft3.
| |
This next problem will provide us with two volumes and a length from similar solids. Example: Determine the length of the base of the small pyramid (marked with an ‘x’) using the information provided within the diagram below.
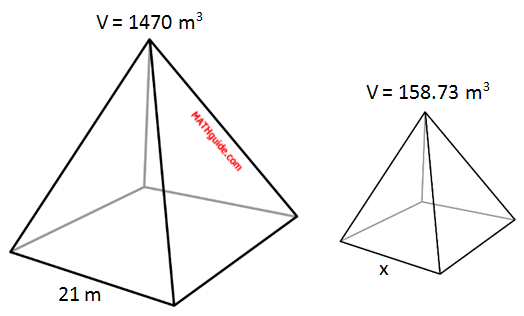
We will organize the information using the mathematical relationship from a previous section (see Relationship Between Lengths and Volumes).
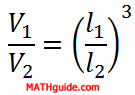
Setting up the ratio as small:big or big:small is arbitrary. For this explanation, a small:big setup will be used. So, the volumes will be placed into the equation, small:big. The 21 will be placed in the denominator of the second fraction because it is a length from the larger solid.
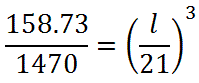
To start solving for the length, we need to cube the right fraction.
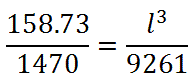
Now, we must cross-multiply (see Proportions).
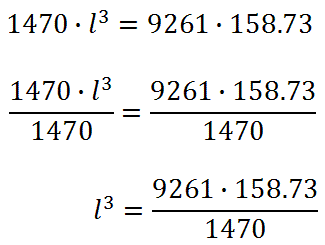
To solve for the length, we have to do the inverse of cubing, which is cube rooting.
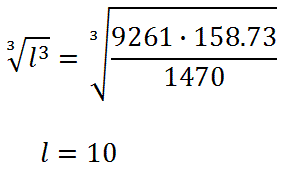
This means the length marked with the 'x' has a length of 10 m.
| |
Try this instructional video. | |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo: