Volume of Common Solids | ||
| ||
Introduction | ||
In this section, you will learn how to calculate the volume of common solids to include:
|
V = sum of all unit cubes | ||||||
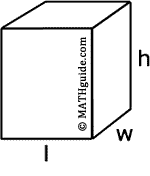
Within our area section, we had to provide a definition for the meaning of area. That definition rested upon the square -- particularly a unit square. We saw the area of a figure was nothing more than the sum of all unit squares of a figure. For the volume of a solid, there is a similar definition. The definition for volume is the unit cube.
A unit cube can be 1" x 1" x 1" or 1 yd x 1 yd x 1 yd or 1 ft x 1 ft x 1 ft or a cube by some other unit.
| ||||||
V = Bh = lwh | ||||||
Let's take a look at a diagram of an actual prism. A diagram will help us understand what volume actually means and how volume is calculated.
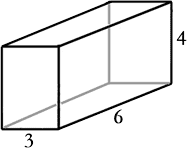
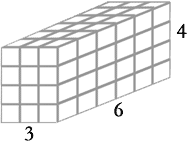
Here is a prism that has a length of 3 units, a width of 6 units, and a height of 4 units.
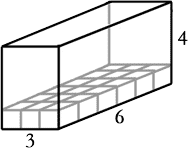
To understand what volume means, let's start by filling the bottom of the prism with unit cubes. This means the bottom of the prism will act as a box and will hold as many cubes as possible without stacking them on top of each other. This is what it would look like.
The diagram above does not yet represent the total volume. It only represents a partial volume, but we need to count these cubes to arrive at the total volume. We could count them one at a time or we could use a shortcut.
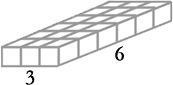
Since the length is 3 units and the width is 6 units, the bottom layer of cubes measure rows and columns that are 3 units by 6 units. So, a quick way of counting the blocks would be to multiply 3 by 6. In general, we would multiply the length of the prism by its width. Multiplying the numbers, we arrive at 18 cubes resting on the prism's base. If we imagine the prism like a building, we could stack cubes on top of each other until the prism is completely filled. It would be filled so that all cubes are touching each other such that no space existed between cubes. It would look like this.
To count all the cubes above, we could use another shortcut. We already know there are 18 cubes on the bottom level and all levels contain the exact number of cubes. Therefore, we need only take that bottom total of 18 and multiply it by 4 because there are four levels to the prism. 18 x 4 = 72 total cubes to our original prism. If we review our calculations, we find that the total bottom layer of cubes was found by multiplying the prism's length by its width. Then, we took the result and multiplied it by the prism's height. So the volume of a prism is its length times its width times its height. Sometimes geometers refer to the volume as the area of the bottom times the height. Symbolicly, it is written as V = Bh, where the capitol B stands for the area of the solid's base (bottom). To understand the units of our answer, we could think in terms of algebra. We know that x times x times x is x3; similarly, units x units x units = units3. So if we had to find the volume of our original cube, all we need to do is multiply 3 units x 6 units x 4 units to get 72 units3 or 72 cubes.
Example 1: If l = 7 ft and w = 5 ft and h = 2 ft, then the volume would be... V = Bh
Example 2: If l = 12 yds and w = 10 yds and h = 1/2 yd, then the volume would be... V = Bh
| ||||||
V = Bh = πr2h | ||||||
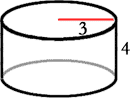
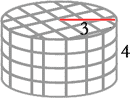
The process for understanding and calculating the volume of cylinders is identical to that of prisms, even though cylinders are curved. Here is a general cylinder.
Let's start with a cylinder of radius 3 units and height 4 units.
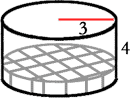
We fill the bottom of the cylinder with unit cubes. This means the bottom of the prism will act as a container and will hold as many cubes as possible without stacking them on top of each other. This is what it would look like.
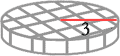
The diagram above is strange looking because we are trying to stack cubes within a curved space. Some cubes have to be shaved so as to allow them to fit inside. Also, the cubes do not yet represent the total volume. It only represents a partial volume, but we need to count these cubes to arrive at the total volume. To count these full and partial cubes, we will use the formula for the area of a circle.
The radius of the circular base (bottom) is 3 units and the formula for area of a circle is A = πr2. So, the number of cubes is (3.14)(3)2 = (3.14)(9), which to the nearest tenth, is equal to 28.3. If we imagine the cylinder like a building (like we did for prisms above), we could stack cubes on top of each other until the cylinder is completely filled. It would be filled so that all cubes are touching each other such that no space existed between cubes. It would look like this.
To count all the cubes above, we will use the consistency of the solid to our advantage. We already know there are 28.3 cubes on the bottom level and all levels contain the exact number of cubes. Therefore, we need only take that bottom total of 28.3 and multiply it by 4 because there are four levels to the cylinder. 28.3 x 4 = 113.2 total cubes to our original cylinder. If we review our calculations, we find that the total bottom layer of cubes was found by using the area of a circle, πr2. Then, we took the result and multiplied it by the cylinder's height. So the volume of a cylinder is π times the square of its radius times its height. Sometimes geometers refer to the volume as the area of the bottom times the height. Symbolicly, it is written as V = Bh, where the capitol B stands for the area of the solid's base (bottom). To understand the units of our answer, we could think in terms of algebra. We know that (x)2 times x is x2 times x, which equals x3; similarly, (units)2x units = units3 for the same reason. So if we had to find the volume of our original cube, all we need to do is multiply π x (3 units)2 x 4 units to get 113.2 units3 or 113.2 cubes.
Example 1: If r = 5 cm and h = 6 cm, then the volume would be... V = Bh
Example 2: If r = 12 ft and h = 2 ft, then the volume would be... V = Bh
| ||||||
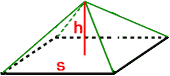
V = ⅓Bh = ⅓s2h | ||||||
To find the volume of a square based pyramid, we will start with a cube, which is a prism that has edges of equal length, which have been labelled with the traditional letter s.
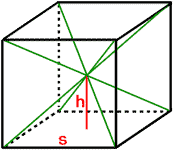
Next, segments will be drawn from each vertex (corner) that will travel through the cube's center to other vertices. In doing so, six congruent (equal) pyramids are created. The volume of the cube can be found by using the formula for a prism, namely V = Bh. So, V = s2 times s = s3.
The volume of each of the pyramids are equal; therefore, their volumes must be 1/6 the original cube's volume. This means each pyramid has a volume, V = s3/6.
By examining the cube with its diagonals, we can see that it takes two pyramid heights to be equal to the base length of the cube, or 2h = s. By substitution, we get V = s3/6 = (s2 times s)/6 = (s2 times 2h)/6. By simplifying the expression, we get V = 2(s2 times h)/6, which is the same as V = 2Bh/6 = Bh/3 or V = ⅓Bh.
Example 1: If s = 3 in and h = 5 in, then the volume would be... V = ⅓Bh
Example 2: If s = 7 m and h = 12 m, then the volume would be... V = ⅓Bh
| ||||||
V = ⅓Bh = ⅓πr2h | ||||||
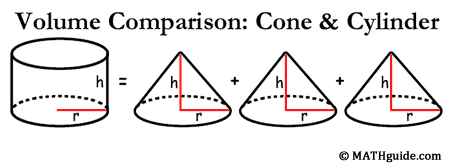
The formula for the volume of a cone can be determined from the volume formula for a cylinder. We must start with a cylinder and a cone that have equal heights and radii, as in the diagram below.
Imagine copying the cone so that we had three congruent cones, all having the same height and radii of a cylinder. Next, we could fill the cones with water. As our last step in this demonstration, we could then dump the water from the cones into the cylinder. If such an experiment were to be performed, we would find that the water level of the cylinder would perfectly fill the cylinder.
This means it takes the volume of three cones to equal one cylinder. Looking at this in reverse, each cone is one-third the volume of a cylinder. Since a cylinder's volume formula is V = Bh, then the volume of a cone is one-third that formula, or V = ⅓Bh. Specifically, the cylinder's volume formula is V = πr2h and the cone's volume formula is V = ⅓πr2h. This same relationship exists between pyramids and prisms. If we were to start with a pyramid and a prism with congruent bases and heights, we would find the exact same ratio of volumes. It would take three pyramids to completely fill a prism. This is why their formulas share the same relationship with that of cones and cylinders. For prisms and cylinders, their volumes are V = Bh. For pyramids and cones, their volumes are V = Bh/3 or V = ⅓Bh.
Example 1: If r = 4 ft and h = 5 ft, then the volume would be... V = ⅓Bh
Example 2: If r = 6 cm and h = 2 cm, then the volume would be... V = ⅓Bh
| ||||||
V = (4⁄3)πr3 | ||||||
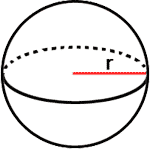
A sphere is the locus of all points in a region that are equidistant from a point. The two-dimensional rendition of the solid is represented below.
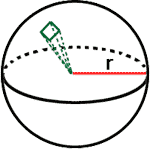
To calculate the volume of a sphere, we must imagine the sphere as an infinite number of pyramids whose bases rest on the surface of the sphere and extend to the sphere's center. Therefore, the radius of the sphere would be the height of each pyramid. One such pyramid is depicted below.
The volume of the sphere would then be the sum of the volumes of all the pyramids. To calculate this, we would use the formula for volume of a pyramid, namely V = ⅓Bh. We would take the sum of all the pyramid bases, multiply by their height, and divide by 3. First, the sum of the pyramid bases would be the surface area of a sphere and the surface area of a sphere is 4πr2. Second, the height of each of the pyramids is the radius of the sphere, r. Third, we divide by three. The result of these three actions is ⅓(4πr2)(r) = (4⁄3)πr3. This is the volume of a sphere.
Example 1: If r = 300 mi (a moon), then the volume would be... V = (4⁄3)πr3
Example 2: If r = 4 mm (a large marble), then the volume would be... V = (4⁄3)πr3
| ||||||
After reading the lessons, try our videos.
| |
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
| |
After reading the lessons, try these activities.
| |
Teachers can use a teacher-directed, Socratic method or a teacher can use cooperative learning. Whether a teacher uses careful direction or provides a few ideas to guide students to the formulas for volume, the discovery approach, with or without assistance, has been shown to be an effective strategy to help students become independant, active learners. As the explanations above for prisms, cylinders, pyramids, cones, and spheres will indicate, the formulas for volume of these solids are attainable through discovery. A teacher can guide students to the formulas using critical questions with relative ease. Students can then be placed in groups and provide these groups with tools necessary for creating their own solids and the respective volume formulas for those solids.
The extent to which students are left discovering these formulas on their own will depend on teacher experience with discovery lessons, student familiarity to discovery exercises, and the maturity levels of students. After students successfully experience the foundations behind the formulas, they will be able to recall these formulas more readily and apply them more accurately.
| |
These are lessons that are related to volume.
| |
 uizmaster:
uizmaster: 
 ideo:
ideo: 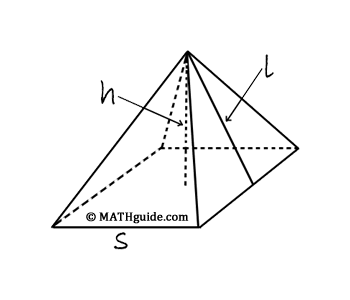
 ctivity:
ctivity: 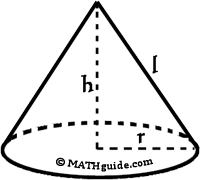
 esson:
esson: