Domain and Range | ||
| ||
Introduction | ||
In this section, you will learn how to determine the domain and range for relations and functions. Here are the sections within this lesson:
|
To get started, let us take a look at the definition of domain:
Now let us takle a look at the definition of range:
The section below will inform you how these definitions are applied on two relations.
| |||||
Here is a basic relation written as a set of points.
Example 1: H = {(-2,3), (-1,0), (0,-3), (1,6), (1,-1), (2,3)} It is not a function because of the two points {(1,6), (1,-1)}. Yet, we can still determine the domain and range of this relation. Recall, the domain is the set of all x-values. Here are the x-values in set H. Domain = {-2, -1, 0, 1, 2} Take care to notice that two '1's were not listed because it is unnecessary to duplicate domain values. Those five values are the only x-values that set H takes on. To determine the range, we must form a set of all the y-values, like so. Range = {3, 0, -3, 6, -1} Notice how the last '3' was not written. It is not necessary to list y-values twice. In fact, some people may list the range in order from least to greatest value.
Range = {-3, -1, 0, 3, 6}
Example 2: (x - 1)2 + (y - 2)2 = 9 To determine the domain and range of this relation, it is helpful to sketch its graph on a coordinate plane.
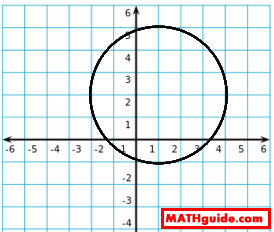
It can be seen that this relation is a circle that has a center at (1,2) and a radius of 3. It is not a function because it does not pass the vertical line test. To determine the domain of this relation, we have to determine how far left and how far right it goes to see which x-values it has. This next image makes that easy to see.
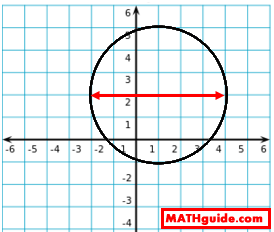
The circle goes as far as -2 to the left and as far as 4 to the right. It also takes on all x-values between -2 and 4. So, we can write the domain like so. Domain = {x | -2 < x < 4} To determine the range, we have to see how far up and how far down the relation goes to see which y-values it has. Look at this next image.
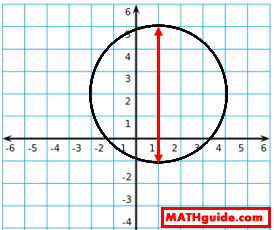
It can be seen that the circle goes as high as 5 and as low as -1 and it takes on values between those extremes. This is how the range can be written. Range = {y | -1 < y < 5} It is clear that once the graph of a relation is gained, the domain and range can be determined.
Use the next section to see videos on determining the domain and range for several functions.
| |||||
View our instructional videos related to domain and range.
| |||||
View our interactive quiz related to domain and range.
| |||||
View activity that addresses domain and range and other concepts/skills.
| |||||
Try this lesson, which is closely related to the lesson above.
| |||||
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: