Testing Relations for Symmetry | ||
| ||
Introduction | ||
In this section, you will learn four tests for symmetry. Here are the sections within this page:
|
A description of symmetry would be this. If a shape -- once turned, flipped, or slid -- is the same as another shape, the two shapes are said to possess symmetry. Symmetry can also be a characteristic of a single shape if it has symmetry with repsect to itself. This picture of a scene reflecting off of a lake possesses horizontal symmetry. The top and bottom of the photo look alike.

The next picture of a female model demonstrates vertical symmetry. The left and right side of the photo look like reflections off a mirror.

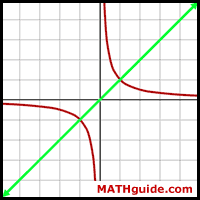
This next picture is a graph of the equation y = 1/x. The reflection line is not horizontal or vertical. This symmetry runs along the diagonal line y = x.
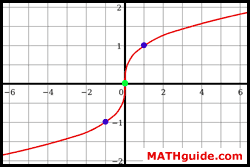
This next graph, which is a cube-root function, has a symmetry across the origin. The symmetry requires us to take any point on the image and reflect it over the origin. Take the point (1,1), which is a blue point above and to the right of the origin. If it is flipped directly across the origin, it lands on (-1,-1). Since (-1,-1) is a point on the curve, it demonstrates this origin (point) symmetry. All points on the cube-root curve reflect on itself.
| |
There are four common tests for symmetry. The procedures for handling these symmetries are detailed within this table.

Use the next section to see how these procedures are used.
| |
Understanding symmetry and carrying out the tests for symmetry requires a bit of concentration. Watch this instructional video on symmetry to learn. | |
Now it is time to see if you understand the lessons above. Try this interactive quizmaster.
| |
Try this lesson, which is closely related to the lessons above.
| |
 ideo:
ideo:  uiz:
uiz:  esson:
esson: