Vectors | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn about vectors. Here are the subsections within this lesson:
|
Architects, engineers, physicists, mathematicians, meteorologists, computer programmers and anyone who desires to know how objects and energies behave and interact learn about vectors. | |
Vectors have been used for a long time. The Pyramids of Giza began construction near 2600 BC. The Pyramid of the Sun in Teotihuacan (Mexico) was completed in 100 AD. Machu Picchu in Peru was built in the 15th Century. Knowledge of levers for moving large weights was essential for moving large stones for all of these constructions.
Formal knowledge of vectors is credited to Archimedes (3rd Century BC) within Heron's Mechanics (1st Century AD). Heron was very clever and with his knowledge of vectors created vending machines, coin operated machines, and steam-powered mechanisms. During the Eastern Han Dynasty (1st and 2nd Centuries AD), these machines were created: agricultural machines with gears, belt-driven machines, link and leverl transmission, and more.
| |
A vector is anything that has both direction and magnitude. Here are some examples that will help you determine when situations do and do not involve vectors. Example 1: A car was traveling at 50 mph going South. The speed is the magnitude and the southerly movement is a direction. This is a vector. Example 2: An electron was traveling at the speed of light. The electron has magnitude, which is the speed of light. However, it does not have a direction. This is not a vector. Example 3: A balloon was traveling upward at 4 mph. The balloon has a direction (upward) and it has a magnitude (speed). This is a vector. Example 4: The man weighed 150 pounds.
This is a tricky problem. It appears that there is no direction. Yet, we know that the direction of the force points downward, toward the center of the Earth. This is a vector because it has direction (downward) and magnitude (weight).
| |
To get an idea of how vectors are used mathematically, it is necessary to use diagrams. The diagrams help us organize information. Here are two vectors both pointing East.

The vector on the top has about twice the magnitude (length) of the vector at the bottom.
The length of the vector can indicate any quantity, but it typically represents speed, force, or pressure.
| |
If a vector is not vertical or horizontal, it is sometimes necessary to break down a vector into horizontal and vertical components. In doing so, it is then easy to see how two or more forces interact with one another. Imagine a vector that has an angle of 75 degrees with a magnitude of 60 mph. This is what it would look like. If you need to review how trigonometric angles are handled, see our lesson called Trigonometric Angles.
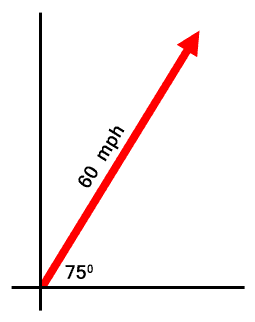
What we need to do is determine the lengths of the horizontal and vertical components of this vector, which is seen in grey below.
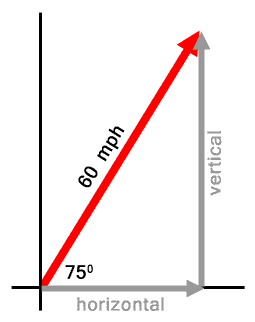
We will need to do some trigonometry. Let's call the horizontal length 'x' and the vertical length 'y.' See below.
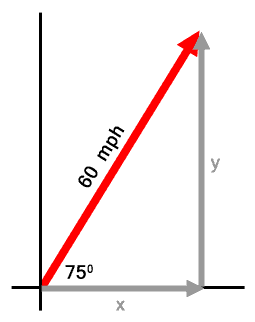
Now we need to solve for 'x' and for 'y.' If you need to first brush up on your trigonometry skills, see our lesson called Trigonometry with Right Triangles.
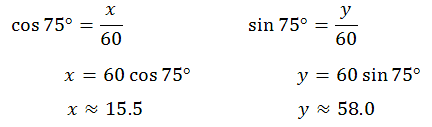
This means the horizontal component is 15.5 mph and the vertical component is 58.0 mph. When we write this vector mathematically, we seperate the horizontal and vertical components with a comma, like so. <15.5, 58.0> If you would like to see a video on this topic, view this link below.
| |
When we write vectors using mathematical notation, there are two different forms. If the magnitude and direction are known for a vector, we:
u = <30, 120o>. If the horizontal and vertical components are known, we:
v = <10, 8>.
| |
When we add vectors, we simply add the horizontal components together and then we add the vertical components together. It is as if we are adding like terms, horizontal values with horizontal values and vertical values with vertical values. Here are two examples. Example 1: Calculate <5, 4> + <7, -4>.
We add the horizontal values together: 5 + 7 = 12. The result is <12, 0>. Example 2: Calculate <-3, 9> + <-8, 2>. The result is <-3 + (-8), 9 + 2>, which is <-11, 11>. Try our quizmaster to ensure you know how to add vectors.
| |
Subtracting vectors is very similar to adding vectors. Subtract corresponding components, horizontal with horizontal and vertical with vertical. Follow these examples to see how vectors are subtracted. Example 1: Calculate <13, -3> - <-4, 8>.
We subtract the horizontal values together: 13 - (-4) = 13 + 4 = 17. The result is <17, -11>. Example 2: Calculate <-12, 4> - <-1, 16>. The result is <-12 - (-1), 4 - 16>, which is <-11, -12>. Try our quizmaster to ensure you know how to subtract vectors.
| |
If we know the components of a vector, we may want to determine the magnitude or length of the vector. For instance, say we are working with this vector: <3, -7> First, sketch the vector.
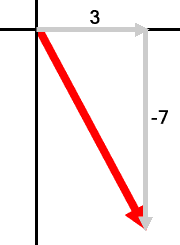
To determine the length of the vector, we really need the length of the hypotenuse. To calculate this length, we utilize the Pythagorean Theorem. We will use the letter 'r' to represent the length of the hypotenuse. The 'r' typically stands for 'radius.'
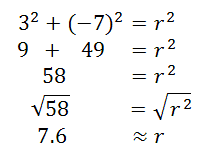
The magnitude of the vector <3, -7>, typically written as |<3, -7>|, is 7.6. Use the links below to access our video and quiz on this topic.
| |
Continuing with the last vector, <3, -7>, let's look at its sketch again.
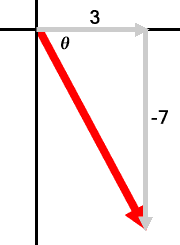
If we need to calculate its direction, we need to first calculate its reference angle. The reference angle has been marked with the Greek letter theta. To do this, we will use the tangent function, like so.
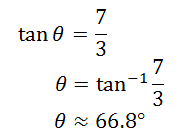
We can now say that the angle of the vector is about 67 degrees south of east. Or, more traditionally, we can use a standard trigonometry angle that begins in to the east and rotates counterclockwise (see our lesson called Trigonometric Angles). In that case our traditional angle would measure 360 - 67 or 293 degrees. Use the link below to access our video on this topic.
| |
Now that we know how to take vectors and calculate their horizontal and vertical components, we can combine two or more vectors. Generally speaking, these are the steps. Let us say you are given two vectors to add. Each vector will have its own magnitude (r-value) and direction (theta, which is a standard trigonometric angle). Combine <r1, θ1> with <r2, θ2>. We have to determine their horizontal and vertical components and write the vectors accordingly. The horizontal component is always equal to rcosθ and the vertical component is always rsinθ. This would make the problem look like this: Combine <r1cosθ1, r1sinθ1> with <r2cosθ2, r2sinθ2>. Combining these two vectors requires us to add horizontal values with horizontal values and add vertical values with vertical values to get this resultant vector.
<r1cosθ1 + r2cosθ2, r1sinθ1 + r2sinθ2>
| |
The last section explained the logistics of combining two vectors. Let us examine a real world problem. Kim and Noah decide to move a large weight by tying ropes to it and pulling it. Kim's rope is at a 130 degree angle and she pulls at 30 Newtons. Noah's rope is at 65 degrees and he pulls with a 40 Newton strength. If we place these two forces together, what is the resultant force on the weight? First, we could use a diagram.
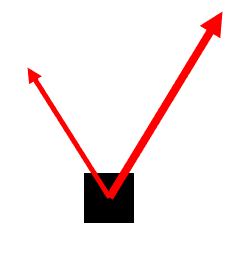
Next, we need to convert their forces to horizontal and vertical components. Let's use k for Kim's vector and n for Noah's vector.
k = <30, 130o> = <30cos130o, 30sin130o> = <-19.3, 23.0>. Now, we add the vectors by combining their respective parts, horizontal with horizontal components and vertical with vertical components.
k + n = <-19.3, 23.0> + <16.9, 36.3> = <-19.3 + 16.9, 23.0 + 36.3> If the magnitude is needed, we utilize the Pythagorean Theorem, like so.
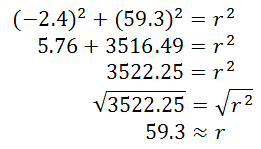
If we require a direction, we can calculate the reference angle using the tangent function, like so.
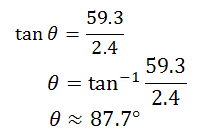
This means the vector has a traditional angle of roughly 180 - 88 degrees or 92 degrees. So, the resultant vector can be written in either of these two forms:
k + n = <-2.4, 59.3> or This means the resultant vector is slightly past 90 degrees and it is about 50% greater in length than Noah's vector. The resultant vector (in blue) has been drawn in the diagram below.
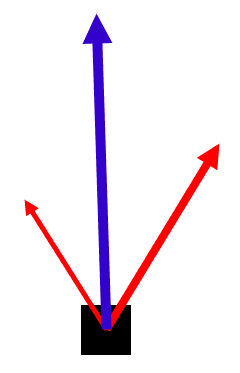
| |
Watch our instructional videos.
| |
Try our interactive quizzes to determine if you understand the lessons above.
| |
Try this activity that ties together paper airplanes, data tables, probability, and trigonometry.
| |
Try these lessons, which are closely related to the lessons above.
| |
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: