Engineering Notation (Vectors) | ||
| ||
Introduction | ||
This webpage will teach you about the engineering notation for vectors. Here are the sections within this lesson page:
|
To understand engineering notation, we must first understand what a unit vector is. A unit vector is a vector that has a magnitude equal to one, which means it has a length of one. If v is a unit vector, then we can express this meaning as...
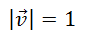
Concerning vectors, the vertical lines around v indicate 'magnitude.'
| |
There are important unit vectors used by mathematicians, physicists, and engineers alike. Here is a horizontal unit vector within the Cartesian plane.
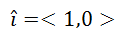
Here is a vertical unit vector within the Cartesian plane.
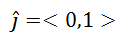
So, what could k mean? If we open up our representation of vectors into space by creating a third axis that is perpendicular [orthogonal means perpendicular] to the coordinate plane, we get a new unit vector, called k.
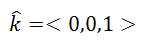
If we are referring to 3-dimensional space, then we could also represent i and j using three values, like so.
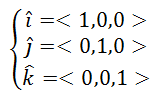
This is what the unit vectors look like in 3-dimensions.
| |
If we were given the vector u=<3,4>, we could sketch it in the Cartesian plane. The vector would be would be drawn so that its tail is at (0,0) and its head is at (3,4), like so.
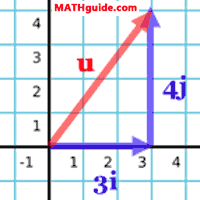
We can see two blue vectors in the diagram. The horizontal vector is comprised of three is. The vertical vector is comprised of four js. When adding the horizontal and vertical vectors, the horizontal vector was drawn first. Then, starting from the head of the horizontal vector, the vertical vector was drawn. The resulting red vector is constructed by starting at the tail of the horizontal vector and ending at the head of the vertical vector. [When adding vectors, we place vectors in a tail to head, tail to head, tail to head fashion.] In other words, we can write the vector u using is and j, like so.
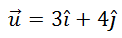
This means there are two synonymous ways to write u.
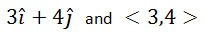
Example: If a = 2i - 4j and b = -8i + 5k, calculate a + b. Add the horizontal components, then add the vertical components. Here is the result: a + b = -6i + j . Example: Sketch w = -4i + 2j.
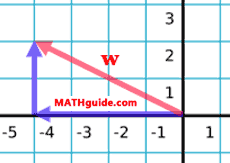
Example: Calculate |w|. We are being asked to calculate the magnitude of vector w. In other words, we have to calculate the length of the vector. Since we are essentially being asked to calculate the length of a hypotenuse and are given two legs of a right triangle (see diagram above), we can use the Pythagorean Theorem, like so.
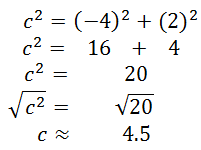
So, |w| is ≈ 4.5.
| |
Try this lesson, which contains the basics of vectors.
| |
 esson:
esson: