Percent Word Problems | ||
| ||
Introduction | ||
This lesson will inform you how to solve percent word problems or problems that contain percents. Here are the sections within this page:
|
Percents are used in a variety of capacities. Here are some common areas:
| ||||||||||||
This is an important question to consider: "What is a percent?" Let us examine the word 'percent.' The word literally means per 100 because cent means 100. So, a percent is a ratio. For instance, 50% means 50 per 100. But, 50/100 is the same as 1/2. Therefore, 50% is equivalent to a half. To gain a visual on what 50% looks like, the glass below is at 50% or 1/2 capacity.

Likewise, 75% means 75/100, which reduces to 3/4. So 75% = 3/4.
Now that you have an idea of what percents mean, we need to look at the word problem portion of percent word problems.
| ||||||||||||
There are certain words that translate to mathematics. Let it be known, this is not always be true. Examine the table below to see the conversion between words and mathematics for the problems that will follow.
When we see either the words 'what,' 'is,' 'of,' or 'percent,' we will substitute their mathematical meaning into an equation. Then, we will solve the equation. Use the three types of problems below to see how it is done.
There are several exceptions to this rule, which will be handled within the section called, The Meaning of Words in Mathematics.
| ||||||||||||
A type 1 problem could look like this.
To solve this problem, we need to convert the problem from words into mathematics. Here is a word to mathematics translation.
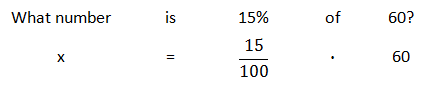
To solve the resulting equation, we progress as follows.
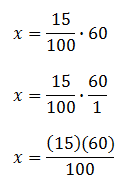
Now, we need to reduce the resulting fraction (or simplify with a calculator).

So, 9 is 15% of 60.
| ||||||||||||
Here is a second type of word problem.
Again, we need to convert this problem into mathematics. Here is the translation.
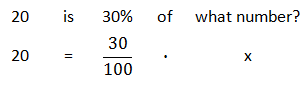
Now, we will solve this equation.
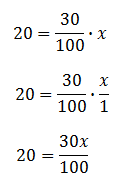
To solve this equation, we have to multiply the coefficient of the x-term by its reciprocal. This means both sides have to be multiplied by this quantity, like so.
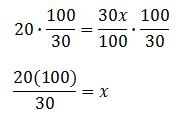
Now, we need to reduce the fraction (or use a calculator) to get our final answer.
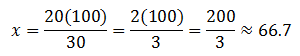
So, 20 is roughly 30% of 66.7.
| ||||||||||||
Here is the last type of word problem.
This sentence needs to be converted into mathematics, like so.
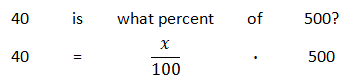
Now, we will solve the resulting equation.
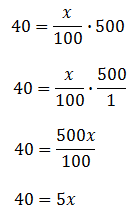
To further solve this equation, we need to divide both sides by 5.
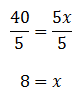
So, 40 is 8% of 500.
| ||||||||||||
The lesson above is a very narrow view of percent word problems. In reality, language does not translate so nicely to mathematics. Here are some examples of the non-routine nature of language and math conversion.
It can be seen how mathematics can be used to solve problems. The key for solving these problems is understanding what the problems means. So, the notion that all problems fit into an easily converted algorithm is not true.
However, the main lesson on this page is designed to give a student the skills to deal with a simple set of conditions. By understanding the simple set of conditions, a student can then add those skills into a growing knowledge base and likely be able to solve a greater number of problems.
| ||||||||||||
Try this instructional video to gain a more personalized view on this topic.
| ||||||||||||
Try this interactive quiz to test your knowledge of percent word problems. | ||||||||||||
 esson:
esson:  ideo:
ideo:  uiz:
uiz: