Reducing Fractions | ||
| ||
Introduction | ||
This lesson will inform you how to reducing fractions. Here are the sections within this lesson page:
|
To simplify fractions it is important to know how to determine factors of a number. It is strongly recommended that you quickly (or not so quickly) review our divisibility lesson before progressing with the following sections.
| |
We use ratios all the time. When we look at pieces of art, we compare lengths to widths. If we buy something in a foreign land, we use ratios to convert the amount into a familiar currency. To travel, we use maps, which are scaled down versions of roads. These are all examples of ratios and ratios often need to be reduced to be most meaningful.
The examples that follow will demonstrate how to reduce fractions.
| |
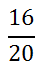
To reduce this fraction, we divide the numerator and the denominator by the same amount. We chose a common factor to do this. The numerator and denominator have a common factor: 2. The division looks like this.
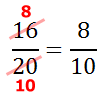
Of course, 8 and 10 also have a common factor, which is again 2.
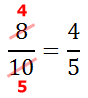
We could have reduced this original problem faster had we noticed the larger common factor, which is 4.
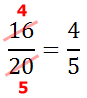
4/5 is the completely reduced solution.
| |
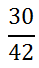
The numerator and the denominator have several factors in common. But, let us start with the most easily recognized. Since the numerator and denominator are both even, they are divisible by 2.
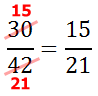
It can be seen that the numerator and denominator are both divisible by 3. So, let us divide the numerator and the denominator by 3.
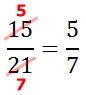
This is the fraction that is completely reduced.
| |
Use this instructional video to learn how to reduce fractions.
| |
Use this interactive quiz to determine if you fully comprehend the sections above.
| |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: