Areas and Lengths of Similar Figures | ||
| ||
Introduction | ||
This lesson will allow you to understand the relationship between area and corresponding sides of similar figures. Here are the sections within this lesson page:
If you are not familiar with ratios, similarity, and proportions, it is strongly suggested that you first review these lessons before proceeding.
|
Question: If a rectangle is twice the size of another rectangle, will it have twice the area? Imagine a rectangle that has a length of 2 feet and width of 4 feet. Using the formula for area, its area would be…
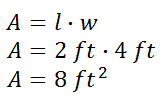
Now, imagine we had another rectangle that was twice as large as large as the first rectangle. Its dimensions would be 4 feet by 6 feet. Let us look at its area.
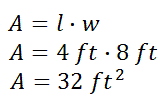
Is the area of the larger rectangle twice that of the small rectangle?
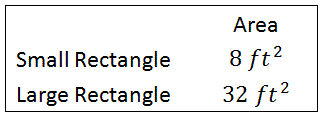
The large rectangle clearly does not have an area that is twice as large as the smaller rectangle. Here is the ratio of their areas, large to small.
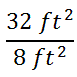
We can reduce this ratio by dividing by common factors.
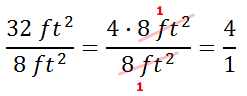
The large rectangle has an area that is 4 times that of the smaller rectangle. This can best be seen by looking at a comparison between the two rectangles.
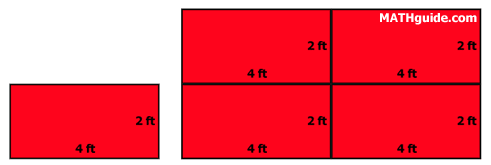
We can see the large rectangle is literally constructed from four smaller rectangles.
The next section will inform you how to find the ratio of areas between any two similar figures.
| |
We first have to establish something important: the notion of similarity. Two figures are similar figures if they have congruent corresponding angles and the ratios of their corresponding sides have equal ratios. [To go into further depth on similarity, see our lesson, called Similar Figures.] Example: Determine the ratio of the areas of these similar figures.
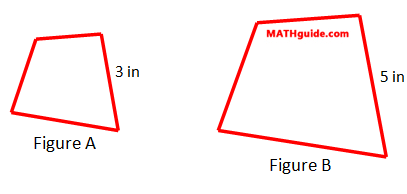
The lengths of two corresponding sides have been provided. They are 5 inches and 3 inches, large to small (written mathematically as large:small). To determine the ratio of their areas, we square the ratio of their corresponding lengths, like so.
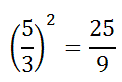
This means the large area is twenty-five ninths the size of the small area. If we reconfigure the lengths, small to large, the ratio looks like this.
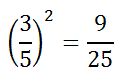
Now we can say that the smaller area is nine twenty-fifths the size of the large area.
Both ratios have equal validity. It is a matter of wanting the ratio large:small or small:large.
| |
The previous section (see Ratios of Areas Between Similar Figures) gave us an important piece of information: the ratios of lengths of similar figures is related to the ratio of the areas of similar figures. However, the relation is the square of the ratio of the lengths is equal to the ratio of the areas. This equation quantifies the relation.
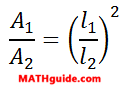
We will need this equation for the example in the following section.
| |
This example will require us to use the equation from the previous section (see The Area and Length of Similar Solids Equation). Example: Determine the area of the large quadrilateral.
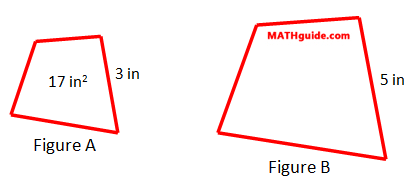
To determine the solution to this problem, we need to make use of a proportion. The following proportion will help us organize the information and determine the area of the large quadrilateral.
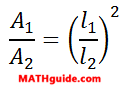
This ratio tells us the ratio of the areas is proportional to the square of the ratio of their respective lengths between corresponding sides. For the sake of solving this example (which is an extension of the first example), we can place numbers into the proportion, small:big, like so.
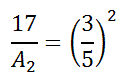
If we square the fraction, we get this new proportion.
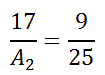
To solve this proportion, we cross-multiply. [See our lesson, called Proportions.]
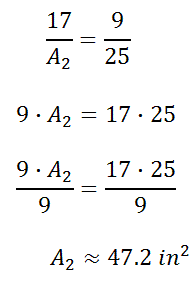
So, the larger area must be 47.2 square inches. The next section will explain how to use a ratio of areas to gain a length. We first have to establish something important: the notion of similarity. Two figures are similar figures if they have congruent corresponding angles and the ratios of their corresponding sides have equal ratios. [To go into further depth on similarity, see our lesson, called Similar Figures.] Example: Determine the ratio of the areas of these similar figures.

The lengths of two corresponding sides have been provided. They are 5 inches and 3 inches, large to small (written mathematically as large:small). To determine the ratio of their areas, we square the ratio of their corresponding lengths, like so.
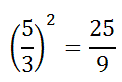
This means the large area is twenty-five ninths the size of the small area. If we reconfigure the lengths, small to large, the ratio looks like this.
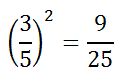
Now we can say that the smaller area is nine twenty-fifths the size of the large area. Both ratios have equal validity. It is a matter of wanting the ratio large:small or small:large. Example: Determine the area of the large quadrilateral.

To determine the solution to this problem, we need to make use of a proportion. The following proportion will help us organize the information and determine the area of the large quadrilateral.
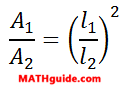
This ratio tells us the ratio of the areas is proportional to the square of the ratio of their respective lengths between corresponding sides. For the sake of solving this example (which is an extension of the first example), we can place numbers into the proportion, small:big, like so.
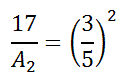
If we square the fraction, we get this new proportion.
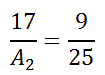
To solve this proportion, we cross-multiply. [See our lesson, called Proportions.]
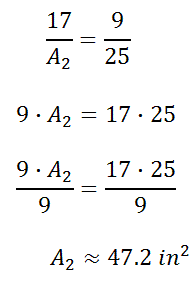
So, the larger area must be 47.2 square inches.
The next section will explain how to use a ratio of areas to gain a length.
| |
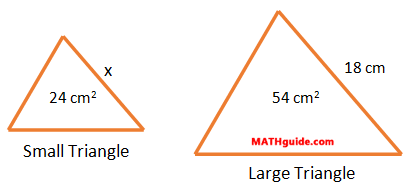
This next problem will start with known areas and one length between two similar figures. Example: Find the x-value within the diagram. The two triangles are similar.
Since we are dealing with areas, we will again use the area relationship.
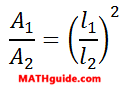
Within this relationship, the areas will be substituted using a small to large ratio.
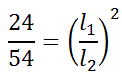
Since the length of 18 cm is from the large triangle, it must go in the denominator to match the large area from the other ratio. Similarly, the 'x' has to go in the numerator because the small area is in the numerator of the other ratio.
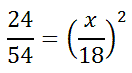
We can square the right ratio, which means to multiply the fraction by itself.
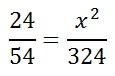
Like all proportions, we have to cross-multiply.
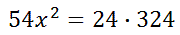
To get the x-term alone, we need to divide both sides by 54.
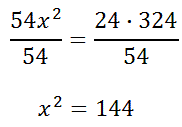
Next, we have to do the inverse of squaring, which is square rooting.
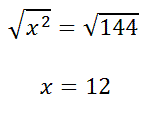
This means the side marked with the 'x' on the smaller triangle must have a length of 12 cm.
| |
Try this instructional video. | |
Try this lesson, which is related to the sections above.
| |
 esson:
esson:  ideo:
ideo: