Similar Figures | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn about similar figures. Here are the topics within this page:
|
Similarity can best be understood by utilizing pictures. Observe these two pictures of bats.

The two pictures look identical, except for their size. The large bat is twice as large as the small bat. This means the width of the large bat is twice the width of the small bat. In fact, all lengths of the large bat are exactly twice that of the small bat. This means the two figures are similar.
To better describe the mathematics of similarity, we need to look at geometric figures.
| |
As we saw within the last section, similar figures are best understood by viewing diagrams or photos that change in size. It is exactly like looking at a map. A map contains roads and boundaries that are like their real life versions except shrunken in scale. Look at these triangles.
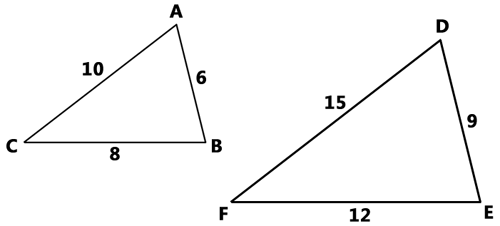
We should notice that the triangles look similar. To determine if they truly are similar, we need to form a ratio of their corresponding sides. If looks like AB and DE match, just like BC and EF match and AC and DF match. Here are the ratios.
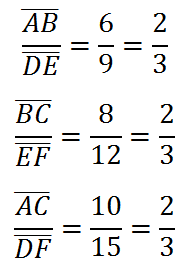
The ratios are all equal to each other, which means that the figures are similar. This means that we can write the similarity in a special fashion, like so.
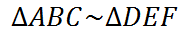
The tilda symbol (~) means 'similar.' The order of the letters also tells us which angles are congruent to each other. The first letter to the left of the tilda matches the first letter to the right of the tilda. The second letters match. Also, the third letters match.
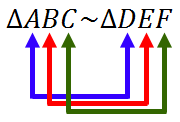
The similarity statement above indicates the following pairs of angles are congruent:
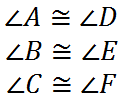
So, we know that two figures that are similar exhibit these two properties:
View this video to see how similar figures are used to find unknown lengths.
| |
In another section of MATHguide, the topic of congruent figures is outlined. Take a look at that section to review five postulates for proving triangles congruent: SSS, SAS, ASA, AAS, and HL. This information can be found within a section, called Geometry Proofs. If we are going to determine if two triangles are similar, we have three postulates: SSS~, AA~, and SAS~. They will be described below.
SSS~

The corresponding sides between the two triangles have the same ratio, which is demonstrated here with this extended proportion.
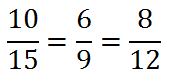
Consequently, this is exactly what SSS~ signifies.
AA~
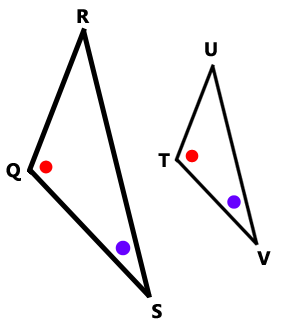
SAS~
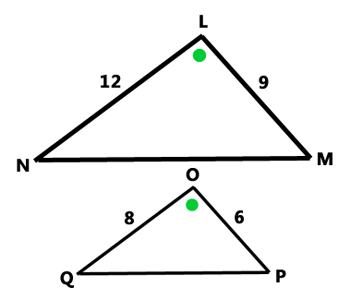
If we form ratios of sides, we get this proportion.
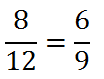
| |
Here are instructional videos.
| |
View these related lessons.
| |
 ideo:
ideo:  esson:
esson: