Conic Sections | |||||||||
| |||||||||
Introduction | |||||||||
In this section, you will learn how to graph conic sections. Here is a list of the sections within this webpage:
| |||||||||
A conic section is a special class of curves. The curves are best illustrated with the use of a plane and a two napped cone. When a plane intersects a two-napped cone, conic sections are formed. The graphic below shows how intersections of a two-napped cone and a plane form a parabola, ellipse, circle, and a hyperbola.
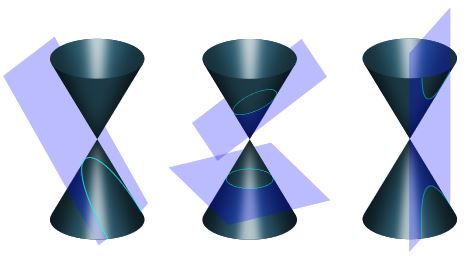 [Credit: Pbroks13]
| |||||||||
Conic sections consist of four general shapes. They are classified as parabolas, circles, ellipses, and hyperbolas. Click on the graphics to learn more about these curves.
| |||||||||
We have seen equations of conic sections in standard form. Now we will look at equations of conic sections in general form. The general form of a conic section looks like this.
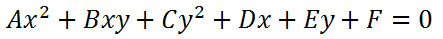
To be able to identify these equations of conic sections in general form, we will make use of a graphic that will help us. The graphic below is called a process flow.

It is called a process flow because the graphic informs us to start at the top and move our way down it. The steps within each level tell us what to do and all we have to do is answer a few questions. To demonstrate how this process flow can be used, follow the example below.
Example:
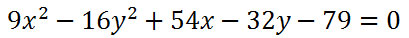
We will work our way down the process flow by starting with level one. It asks, "Is there only one squared term?" Let us examine the equation to answer the question.
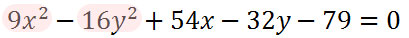
Since our problem has two squared terms, we have to say "no." So, it is not a parabola and we have to go on to level two as directed. Level two asks, "Are the coefficients of the squared terms equal?" Again, we need to look at the equation to answer.
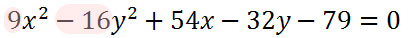
After reviewing the coefficients, we have to say they are not equal. 9 is not equal to -16. So, it's not a circle and we have to proceed to level 3, as directed by the graphic. Level three asks, "Are the coefficients of the squared terms opposite in sign?" Let's examine the graphic again.
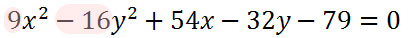
The answer is "yes." 9 is positive and -16 is negative. They do have opposite signs. They are not opposite in value, but they are opposite in that one is positive and the other is negative. According to the process flow, the conic section is a hyperbola. It is clear that it is necessary to know basic terminology to use this process flow. Phrases like squared term, coefficient, and opposite sign need to be fully grasped to benefit by the graphic. Test your ability to use this process flow. Make use of this quiz. | |||||||||
The last section, called Identifying Conic Sections in General Form, demonstrated how to identify conic sections that are written in general form. This section will go one step further. It will explain how to algebraically manipulate the general form of a conic section into standard form.
In order to manipulate these equations, it is necessary to know what the equations of conics look like in standard form. View the table below to better grasp what standard form looks like.

The following video will provide step by step instructions along with an example. The example targets the equation of a hyperbola.
| |||||||||
Here are videos related to the lessons above.
| |||||||||
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
|
Here are activities related to the lessons above.
|
Here related lessons to view.
|
 uiz:
uiz:  ideo:
ideo:  ctivity:
ctivity:  esson:
esson: