Ellipses | ||
| ||
Introduction | ||
In this section, you will learn how to graph ellipses. Here is a list of the sections within this webpage:
|
An ellipse is defined as a set of points in a plane such that the sum of the distance from two fixed points remains constant. Many people would describe the shape of an ellipse as being oval or close to the outline of an egg shape. This is the equation of an ellipse in standard form.
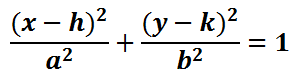 The location of the center of the ellipse is a point located here.
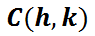 The location of the extreme points, called vertices, are located at these points.
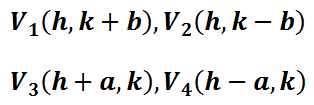 The locations of special points called foci are located according to these rules.
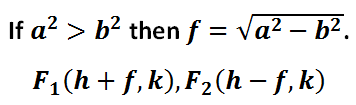
Foci are important points within an ellipse. Foci are important reflective points that are used by architects for theaters and doctors dealing with kidney stones. Johannes Kepler also described the motion of planets using ellipses for the paths of planets and one focal point for the location of our sun.
Use the lesson below to learn how to graph an ellipse, its center, vertices, and foci.
| |
Here is the equation of a specific ellipse written in standard form.
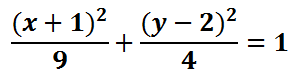 In order to graph the ellipse, we need to first locate its center. Its center is obtained by looking at the numbers inside the parentheses.
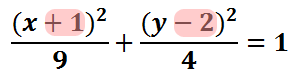 Inside the parentheses with the 'x' there is a 1. Inside the parentheses with the 'y' there is a -2. The center of the ellipse is gained by taking the opposite of these values.
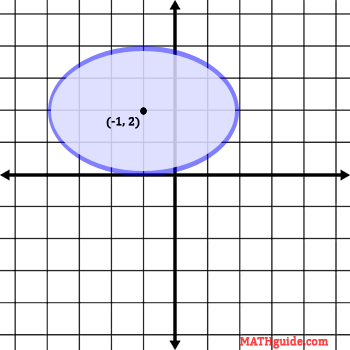
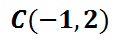 The graph below contains the center of the ellipse and the graph of the ellipse. However, we will go through all the steps required to graph the ellipse. The first step is to acquire the center.
 To proceed, we need to look under the x2-term.
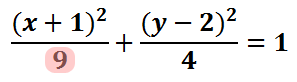 This term is the a2 term, if we review the standard form of the ellipse.
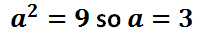 The value of 'a' is 3; since it was gained from underneath the 'x-value,' we move 3 units left and right from the center to locate two vertices. Here is a picture of those vertices.
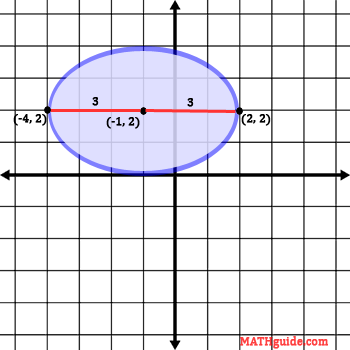 To locate the other two vertices, we have to look at the number underneath the y2-term.
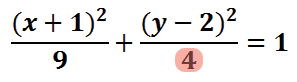 This term is the b2 term, if we review the standard form of the ellipse.
 The value 'b' is 2; since it was gained from underneath the 'y-value,' we move 2 units up and down from the center to locate two more vertices. Here is a graph of those vertices.
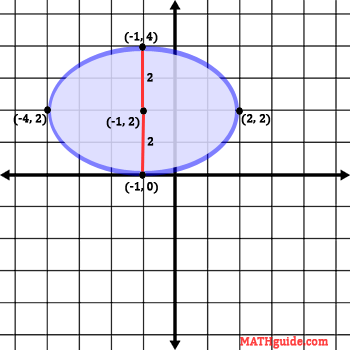 The next steps for graphing this ellipse requires us to know where the major axis is located. The major axis, seen in red below, is the longest distance across the ellipse, which happens to be 6 units in length. The minor axis, seen in yellow below, is the shortest distance across the ellipse, which happens to be 4 units in length.
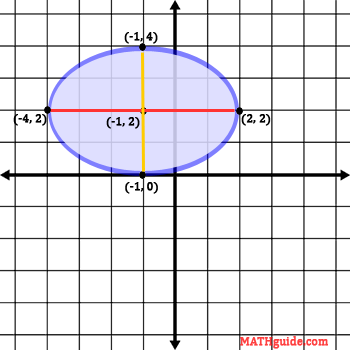 The foci are located across on the major axis, seen in red directly above. To locate the foci, we need to look at both values in the denominator from the original equation.
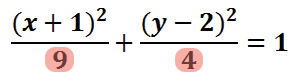 The formula for the foci requires us to take the larger of the two values and subtract the smaller, all while underneath a square root.
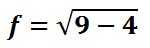 Simplifying further, we get this exact value.
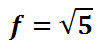 The approximation of this value is as follows.
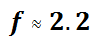 We are now going to use this value and move left and right on the major axis to locate the foci.
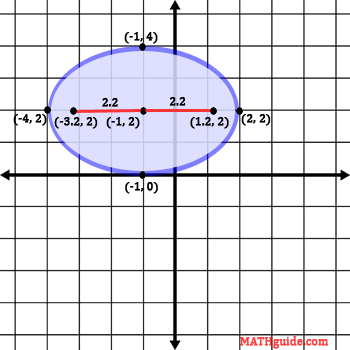 Here are the exact calculations for those foci.
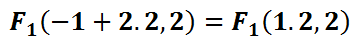
Here is the final graph of the ellipse with all the special points included.
 Try our quizmaster and activity on graphing ellipses below to see if you can graph your own ellipse.
| |
Here are videos related to the lessons above.
| |
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
| |
Here are activities related to the lessons above.
| |
Here related lessons to view.
| |
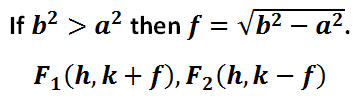
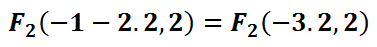
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: