In this section, you will learn how to:

• Definition of a Polynomial
• Adding Polynomials
• Subtracting Polynomials
• Multiplying Polynomials
• Dividing Polynomials: Synthetic Division
• Instructional Videos
• Interactive Quizzes
• Related Lessons

   The definition of a polynomial is not easily explained because it involves several special terms. Knowing these terms is crucial.

Term	Definition	Example in Red
coefficient	It is a constant that is either alone or being multiplied by an expression.	3x5 and -7x2y
exponent	It is the power to which a number or expression is being raised.	62 and (-2c)3
integer	It is a number that contains no fractional or decimal part.	5 and -300

   Now we are ready to understand the definition of a polynomial.

   Definition: A polynomial is an expression composed of coefficients and variables under addition, subtraction and multiplication and exponents on those variables must be non-negative integers.

   This table will help you discern the difference between polynomials and non-polynomials.

Example	Polynomial or Non-Polynomial
4a3	Polynomial
3x-2	Non-Polynomial
-5z2/3	Non-Polynomial
2x2 + 3x - 5	Polynomial

   When adding polynomials, like terms must be combined. For instance, 3c and 5c can be added to get 8c. Likewise, 3x²y and -7x²y can be added to get -4x²y. However, 5x³y and 10x²y⁵ cannot be added together because they do not have the same exact variables and the exact powers on those variables.

   Let those examples guide us regarding the following problem.

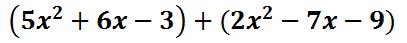   The best way to handle this is to perform the task vertically, instead of horizontally, while aligning like terms.

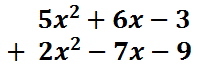   With this arrangement of polynomials, it's easier to determine which terms to combine together.

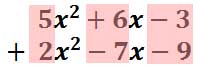   Consequently, here is the solution.

      ideo: Adding Polynomials
      uiz: Polynomial Addition

---

   On this next example, care has to be taken.

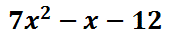
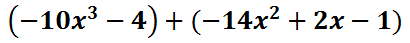   The reason for care is due to the first polynomial. It is missing an x-squared term and an x-term. This is why place-holder terms must be included.

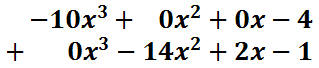   The vertical placement below emphasizes the correct alignment of like terms to be added.

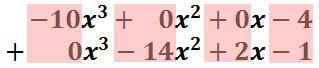   Consequently, the solution is...

      ideo: Adding Polynomials
      uiz: Polynomial Addition

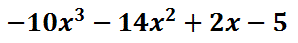
   When subtracting numbers, it is possible to change the problem to addition. Here is a case in point.

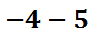   This problem can be changed to an addition problem. All we have to do is switch the subtraction to addition and then change the second number to its opposite, like this.

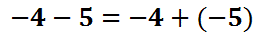   When problems are converted into addition, they are usually done more successfully. The answer is -9, which is harder to obtain as a subtraction problem. When dealing with polynomial subtraction, we can do the exact same process. Here is an example of a subtraction problem with polynomials.

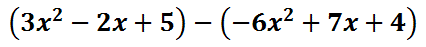   We can also change this problem to addition. Change the subtraction to addition and then switch the last polynomial to its opposite. Our new example would then be

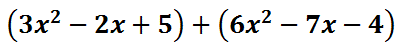   Notice how the second polynomial changed. The -6 changed to 6. The 7 changed to -7 and the 4 changed to -4. Now, the problem is a polynomial addition problem, which is best accomplished vertically.

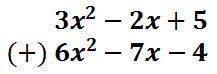   The answer can be gained by adding like terms. The like terms are those that have the same variables and powers on those variables. This vertical form makes it easier to find and add those like terms.

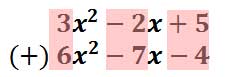Combining those highlighted like terms gives us the following solution.

      ideo: Subtracting Polynomials
      uiz: Polynomial Subtraction

---

   Here is another problem, but this one is in vertical form.

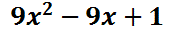
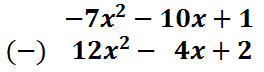   We still have to change this problem to addition. We first have to realize it means we are subtracting the bottom polynomial from the top polynomial. So, we have to take the opposite of the second (the bottom) polynomial. This would give us this addition problem.

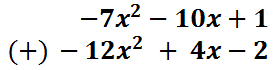   Notice that the last polynomial, the bottom polynomial, was changed to its opposite. Now, we simply add like terms and the like terms have already been aligned.

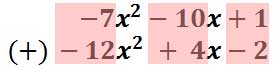   After we add like terms, we will get this solution.

      ideo: Subtracting Polynomials
      uiz: Polynomial Subtraction

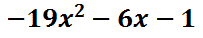
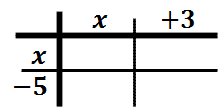
   The best way to multiply polynomials is to do so using a visual organizer. We used a visual organizer in grammar school, called a multiplication table. That is exactly what needs to be used for polynomial multiplication. For example, we will multiply these binomials. [A binomial is a polynomial that has two-terms, bi nomial.]

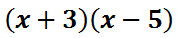   To do this, we will place the first polynomial on the top of our table and the second on the side of our table. [Some people use the method called FOIL instead. However, FOIL only works for binomials and is useless for other types of polynomial multiplication problems.]

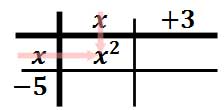
   Now, we will multiply a column times a row. We will multiply x times x and get x² and then place that in the table.

   Likewise, we will multiply x times -5 to get -5x. We will put that in the table.

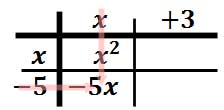   For our last column, we will begin by multiplying "3" times "x." The result is this.

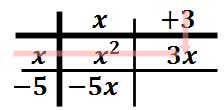   The last item of the table is gained by multiplying "-5" times "3."

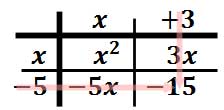   This leaves us with the following table of elements.

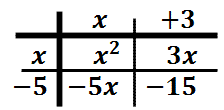   This process has left us with four terms inside the table.

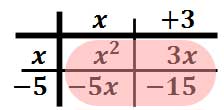   There are two elements within the table that are like terms and they need to be combined together. These are the two like terms.

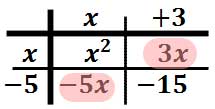   If we write out these four elements horizontally, we get this polynomial.

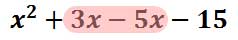   We need to combine the inner-most terms, which are the like terms. After adding the "3x" and the "-5x," we get this solution.

      ideo: Multiplying Polynomials
      uiz: Polynomial Multiplication

---

   For our next example, we will look at a much more difficult problem. We will multiply a binomial times a trinomial.

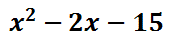
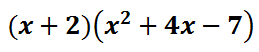   Again, we will place these polynomials on the outside of a table. Place the first along the top and the second along the side.

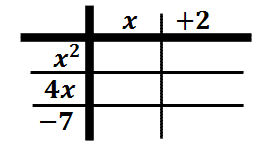   Now, we will begin the process of multiplying columns times rows to gain elements inside the table. Let's start with "x²" times "x" to get "x³."

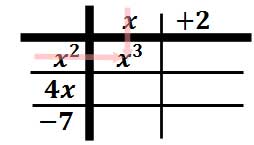   Multiply "x" times "4x" to get "4x²."

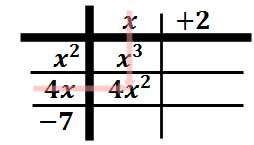   Multiply "x" times "-7" to get "-7x."

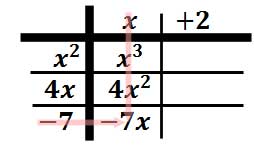   Multiply "2" times "x²" to get "2x²."

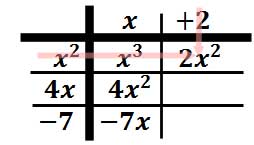   Multiply "2" times "4x" to get "8x."

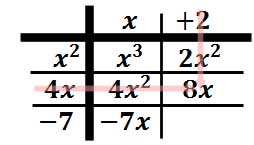   Multiply "2" times "-7" to get the final element in the table, which is "-14."

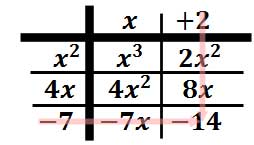   Alright. We have a completed table! We are almost done.

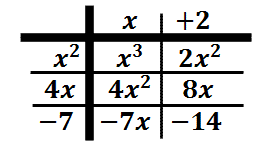   Notice there are six elements within our table. These elements will be used to gain our solution.

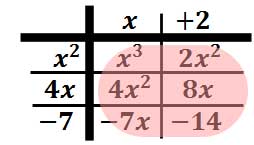   The six elements will be simplified to produce the solution. Notice, however, there are like terms that need to be combined. These like terms have like powers and have been color-coded below.

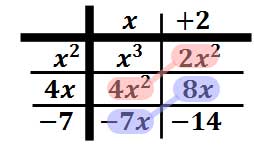   Taking the elements of the table out and writing them horizontally, we get this unsimplified polynomial. Like terms have been color-coded.

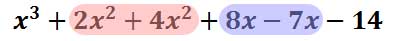   We will combine the like terms by adding "2" with "4" and then adding "8" with "-7." This is the solution.

      ideo: Multiplying Polynomials
      uiz: Polynomial Multiplication

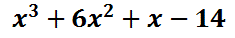
   This video will explain how to divide polynomials using a special technique, called synthetic division.

      ideo: Dividing Polynomials: Synthetic Division

   Try our quizmaster to see if you understand how to divide polynomials by synthetic division.

      uiz: Synthetic Division with Details
      uiz: Synthetic Division

   After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:

      ideo: Adding Polynomials
      ideo: Subtracting Polynomials
      ideo: Multiplying Polynomials
      ideo: Dividing Polynomials: Synthetic Division

   After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:

      uizmaster: Polynomial Addition
      uizmaster: Polynomial Subtraction
      uizmaster: Polynomial Multiplication
      uizmaster: Synthetic Division with Details
      uizmaster: Synthetic Division
      uizmaster: Polynomial Graphs to Factors

   After reading the lessons, try this lesson.

      esson: Factoring
      esson: Complex Numbers
      esson: PARCC Exam Problems and Solutions
      esson: Solving Complicated Proportions