Trigonometry with Right Triangles | ||
| ||
Introduction | ||
In this lesson, you will learn how to use the three basic trigonometric functions to solve right triangle trigonometry problems. If you have not already familiarized yourself with the basics of trigonometry, please visit the page before proceeding. Below, you will find a problem dealing with:
|
The first step is to draw a picture. To do that, we have to know what is meant by an angle of elevation. It is an angle that is measured up from the horizon. From a horizontal line, the 40 degree angle will be measuring an upward angle. This takes us to this diagram.
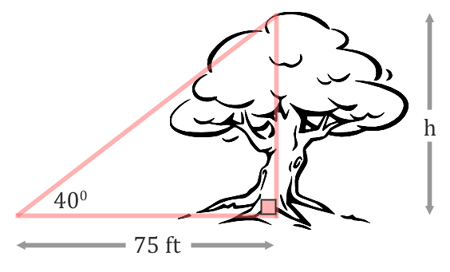 The next step is about labeling the sides. The height of the tree, h, is the opposite side of the triangle. 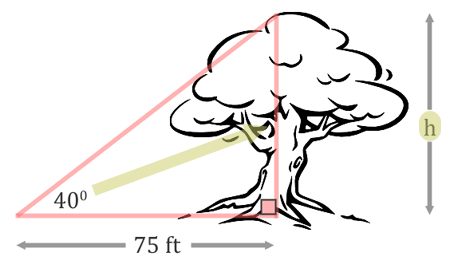 The 75 feet is the adjacent side of the triangle because it is next to the angle. 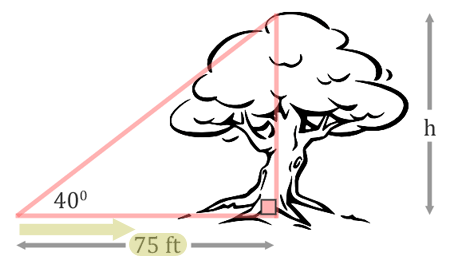 Since we are dealing with the opposite and the adjacent sides of the triangle, not the hypotenuse, we must be dealing with the tangent function. The tangent function is defined as opposite over adjacent (see the three main trigonometric functions for details). We will set up our ratio accordingly for tangent.
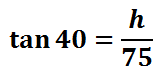 To solve this equation, we will treat it like a proportion by placing a one under the tangent function. Doing so, we can now cross-multiply.
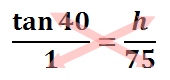 This is the result of cross-multiplying.
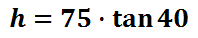 We can now plug this information into a calculator to get the solution.
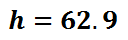 This means the tree is 62.9 feet tall. Now that you have examined this problem, view a related video and quiz.
| ||
As with all trigonometry problems, it is important to get a diagram. Having a diagram will help set up an equation. This is what the problem looks like.
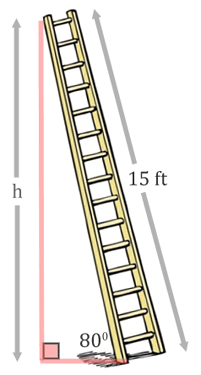 Let's identify the sides. The length of wall, labeled with the 'h,' is the opposite side.
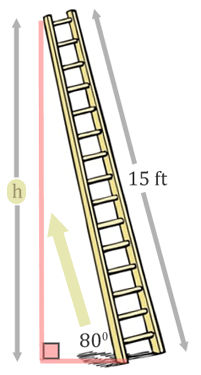 The side opposite the right angle, the 15-feet, is the hypotenuse.
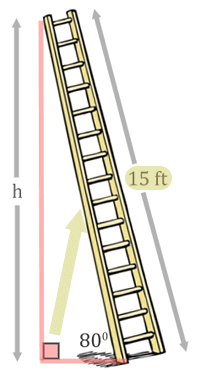 Since we have the opposite and the hypotenuse, we are dealing with the sine trigonometry function (see the three main trigonometric functions for details). We will set up the sine ratio.
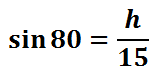 To solve this, we will treat it like a proportion by placing a one underneath the sine function. Then, we will cross-multiply.
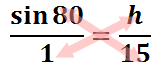 The cross-products give us this.
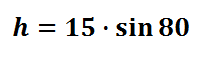 Plugging the information into a calculator will yield the final result.
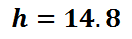 This means the ladder can reach 14.8 feet up a wall. The 0.8 feet is really 9.6 inches (0.8 x 12); so, the ladder reaches up approximately 14 feet and 9.6 inches high along a wall. Now that you have examined this problem, view a related video and quiz.
| ||
we have to get a diagram in order to organize the information and to get a feel of the situaiton. We have to understant the term 'angle of depressin' to be able to place this into a diagram. It means the pilot is looking straight out to the horizon and then he slowly looks down. So, it's a downward angle out from a starting horizonal position. That is why the diagram below has a horizontal line at the top and the 7 degrees is below it.
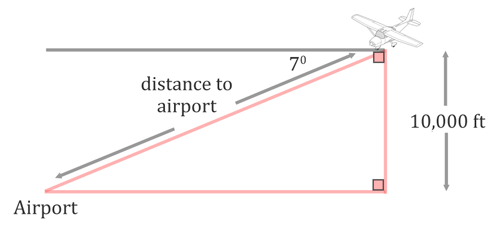 The term altitude is how high the plane is up in the sky, which is why it is represented as a vertical distance in the diagram. To determine the angle inside the triangle, we will take 7 degrees from 90 degrees. The result, 83 degrees, is the angle between the line of sight to the airport and the altitude, as is shown in the diagram below. We also need to mark the distance to the airport with a letter. The letter 'd' has been used.
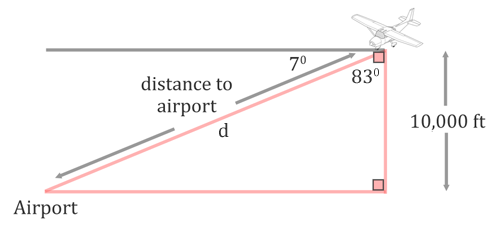 With respect to the 83 degree angle, the 10,000 altitude is the adjacent side.
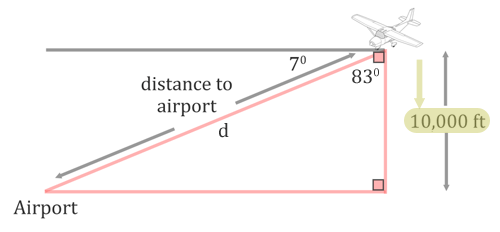 The distance to the airport is opposite the right angle. So, it is the hypotenuse.
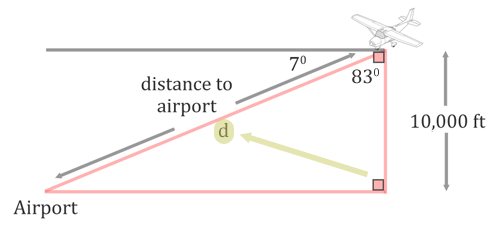 We are dealing with the adjacent side and the hypotenuse. This is why we will use the cosine function (see the three main trigonometric functions for details). We will set up a cosine ratio below.
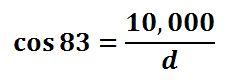 To solve this equation, we will create a proportion by placing a one under the cosine function. Then, we will cross-multiply.
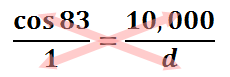 This is what the cross-products look like.
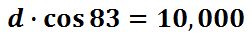 To isolate the variable 'd,' we need to divide both sides by cos 83.
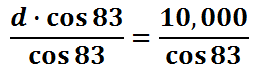 This is the result of our equation.
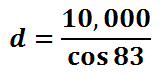 Pluggin this into a calculator, we get this value for 'd.'
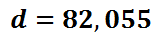 This means the pilot and the plane were 82,055 feet away from the airport. Since every mile is 5,280 feet, the pilot is about 15.5 miles from the airport. Now that you have examined this problem, view a related video and quiz.
| ||
View these instructional videos to assist you with learning right triangle trigonometry:
| ||
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
| ||
We would like to invite you to learn from our advanced trigonometry sections. In these sections, you can learn details that require their own lesson pages.
| ||
 ideo:
ideo:  uizmaster:
uizmaster:  esson:
esson: