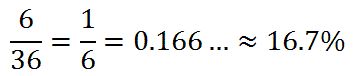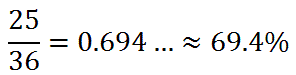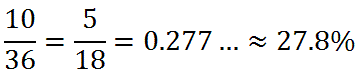Probability Basics | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn how to calculate basic probability problems. These topics will be presented here:
|
Probability is the quantification of determining the likelihood of an event. What does probability mean to car manufacturers? Car manufacturers extend new car customers warranties. These warranties protect the owner in case something breaks, like non-wear and tear items, such as: transmission, engine, and electrical systems. If one of these major systems gets damaged while a car is under warranty, the car will be fixed for free. Car buyers like this protection because it gives them a sense of comfort buying a new automobile.
These probabilities are important in several industries other than the automotive industry. An entire branch of mathematics, called actuarial science, exists to calculate risk for many industries. Actuaries study risk for insurance, finance, and government programs involving mortality. retirement, and predicting the future. Actuaries are respected and well paid.
| |
The lesson that follows demands you already know the following lessons. If you are unfamiliar with these lessons, it is strongly suggested you review them first before proceeding.
| |
The calculation for probability involves counting events. The probability of a certain event, called event A, is written as P(A). Probability is then calculated as follows.
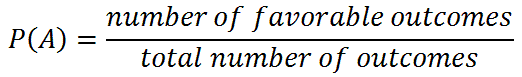
The examples below will run through a variety of circumstances that will demonstrate how to use this formula.
| |
There are many games that use a spinner: like Twister, Life, and Mousetrap. A player spins the arrow on a spinner, the spinner goes wildly in circles, and then the arrow lands on a space. We will use the spinner found below to do several examples using the formula for probability.
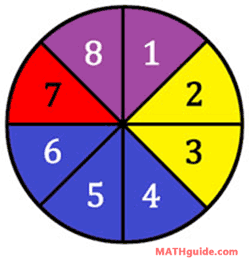
Example 1: Calculate P(spinning 2). There are eight possible outcomes, {1,2,3,4,5,6,7,8} if we only look at numbers and not colors. The number two is one of those numbers. So, the probability is...Example 2: Calculate P(spinning a number < 3). There are two numbers less than 3, namely {1,2}. There are eight possible outcomes {1,2,3,4,5,6,7,8}. So, the probability is...Example 3: Calculate P(an even blue number). Favorable outcomes will be both blue and even numbers. The blue numbers that are even are {4,6}. So, there are 2 favorable outcomes out of 8 possible outcomes.Try our quizmaster to see if you fully understand this lesson. | |
Probability problems would not be complete if we did not look at a bag of marbles. Marble bag problems are typically found in math textbooks and they do a great job demonstrating the need to be an accurate counter. We will use the marble bag below to demonstrate how marble bag problems work using the formula for probability.
Example 1: Calculate P(pulling a red marble). There are three red marbles. There are a total of ten marbles in the bag. The probability is therefore...Example 2: Calculate P(pulling a green marble). There are four green marbles. There are a total of ten marbles in the bag. The probability is therefore...Example 3: Calculate P(pulling a yellow, blue, or red marble). There is 1 yellow, 2 blue, and 3 red marbles. We have 6 marbles that can be pulled that are considered favorable outcomes. There are a total of ten marbles in the bag. The probability is therefore...Watch our video and try our quizmaster to see if you fully understand this lesson.
| |
Most board games include dice, which means most people have seen 6-sided dice, like these.
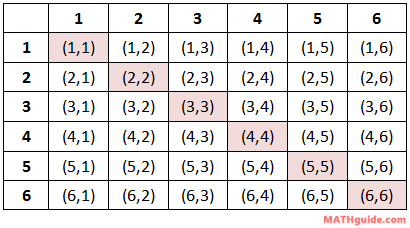
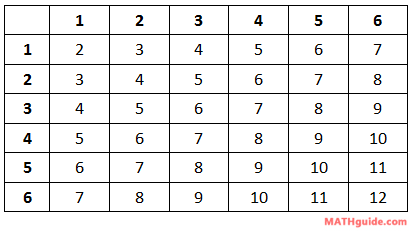
When we roll a 6-sided die, the possible outcomes are {1,2,3,4,5,6}. Calculating probabilities using the formula for probability with a single die are relatively simple because they are similar to spinner problems. However, let us look at what happens when we roll two dice and record the outcomes. Let this table reveal the possible outcomes.
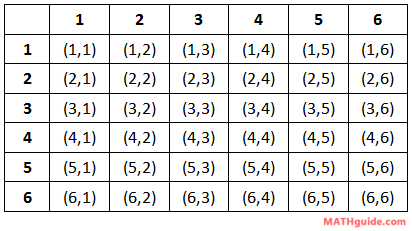
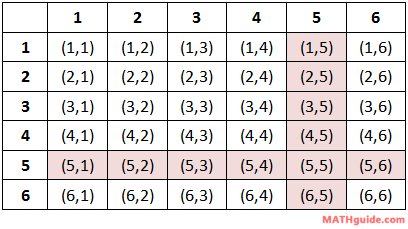
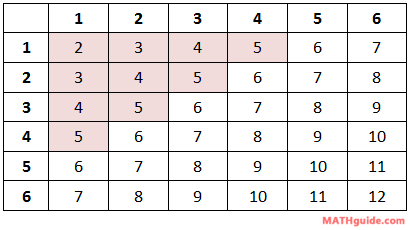
We will use this table to determine the probability problems below. Example 1: Calculate P(rolling doubles). There are six cases when doubles are rolled, which are highlighted below.Example 2: Calculate P(not rolling any 5s). If we cannot roll any fives, let's look at the cases that involve fives, highlighted below.Example 3: Calculate P(rolling a sum < 6). We have to re-examine the die-rolling table so that it reflects dice sums, as follows.Use these resources to solidify your understanding of dice problems.
| |
Try our instructional videos to help learn this material.
| |
Try our interactive quiz to determine if you understand the lessons above.
The quiz below is actually an interactive experiment involving three cars that compete in a professional drag race. Use your knowledge of probability to determine if a certain car has an advantage over the others if they compete two at a time in elimination.
| |
Try these lessons, which are closely related to the lessons above.
| |
It is therefore very important that car companies know how long their car parts will last. They need to know the likelihood of a part failing before a warranty expires. If the part is too likely to fail before the expiration of the warranty, it will cost the car company money to repair the part and it may also make the customer feel hesitant to buy a car from the manufacturer.
esson: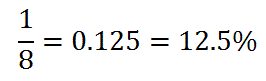 
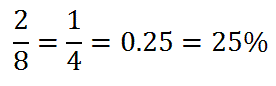
uiz: 
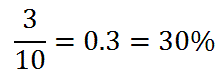
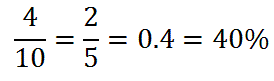
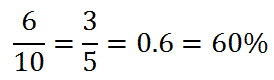
ideo: 
