Combining Vectors | ||
| ||
Introduction | ||
There are a variety of situations when two or more vectors act together in the same situation. This lesson will inform you how to take those vectors, combine them, and determine the resulting vector, called the resultant vector. Here are the subsections within this lesson:
|
For instance, car manufacturers need to know how their products will respond in strange situations, like turning on curves under strange road conditions that involve car velocities and unequal friction occurring on the tires.
Computer programmers, along with properties of physics and meteorology (temperature, pressure, wind speed, ...), create mathematical software models. These models are used to predict the weather. Several models are often accessed especially when strange weather phenomena are possible, like tornados, hurricanes, and blizzards.
| |||
There is a step-by-step approach to combining vectors. These steps will be implemented within the two sections that follow. So, you may have to refer to this step-by-step approach until you become familiar with it.
| |
Imagine a situation where two movers, Gino and Lucia, are pulling on a safe with ropes. If Gino pulls 150 lbs of force at 330° and Lucia pulls at 80 lbs of force at 50°, what is the combined effect?
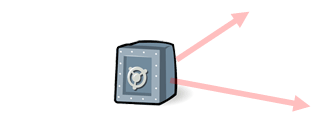
To solve this problem, let's follow the steps that were outlined in the previous section. We will get the components of each vector. The components form of Gino's vector is <150cos(330°), 150sin(330°)>, which comes out to be <129.094, -75>. The component form of Lucia's vector is <80cos(50°), 80sin(50°)>, which comes out to be <51.423, 61.284>. To get the components of the resultant vector, we need to add the horizontal components. Then, we need to add the vertical components separate from the horizontal components, like so.
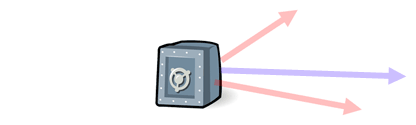
r = < 129.094 + 51.423, -75 + 61.284> To determine the magnitude of the vector (written as | r |), we use the Pythagorean Theorem and the components of the resultant vector, like so.
| r |2 = (181.327)2 + (-13.716)2 Next, we have to find the direction of the resultant vector. By looking at its components, we can see it points right and down, which is akin to the fourth quadrant. To determine the reference angle (represented as alpha), we need to utilize the tangent function, but strip the components of their signs, like so.
tan(α) = (13.716 ÷ 181.327) To find the standard trigonometric angle, we need to subtract the reference angle from 360° because it is akin to being in the fourth quadrant. θ = 360° - 4.326° = 355.674° This means the resultant vector is 181.845 lbs at 355.674°.
| |
Suppose we make our safe-moving problem from the previous section more interesting. Let's add a third mover to the situation. Now there is Sofia pulling on the rope with 70 lbs of force at 10°.
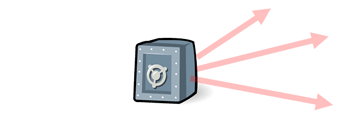
We need to find the component form of her vector. <70cos(10°), 70sin(10°)> We have the component forms of the first two movers, Gino and Lucia. Now we can add Sofia's to the list.
<129.094, -75> is Gino's vector. The new resultant vector will be calculated by adding the horizontal components separate from the vertical components.
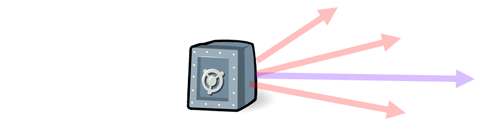
r = < 129.094 + 51.423 + 68.937, -75 + 61.284 + 12.155> Next, we must determine the magnitude of the resultant vector.
| r |2 = (249.454)2 + (-1.561)2 Last, we need to determine the reference angle (alpha) and from that the standard trigonometric angle.
tan(α) = (1.561 ÷ 249.454) By looking at the components of the resultant vector, we can see it is akin to being in the fourth quadrant because it goes right and then down. So, we need to convert the reference angle of a fourth quadrant angle by subtracting it from 360°. θ = 360° - 0.359° = 359.641° So, the resultant vector is 249.459 lbs at 359.641°.
| |
Try our interactive quizzes to determine if you understand the lessons above.
| |
Try these lessons, which are closely related to the lessons above.
| |
 esson:
esson: 
 uiz:
uiz: