Calculating Value Over Time | ||
| ||
Introduction | ||
This lesson will inform you how to calculate the value of items as they change over time. Here are the sections within this lesson page:
|
As we examine different items, we will notice they change in value over time. Some items go up in value. Other items go down in value. Rarely do items remain the same. For instance, cars are notorious for declining in value at steep rates once they are driven off the dealer's lot. Clothing, furniture, and electronics also usually decline in value as time passes. However, there are many items that increase in value over time. The value of land, comic books, precious stones/metals, and homes go up over time -- usually.
The sections that follow will help you learn how to quantify the values of items over time.
| |
The formula for calculating value over time is this.
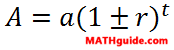
The a-value is the starting value of the item. The A-value is the final value of the item after time passes. The r-value is the rate, written as a decimal value. Last, the t-value is time. Note: the rate and time have to be in the same unit of measure. Typically, the rate is an annual rate and time is measured in years.
The two examples that follow will inform you how to use this formula.
| |
Here is a problem dealing with a car. A new Corvette was worth $12,000 in 1980. If it depreciated at a 1.5% annual rate, how much was it worth in the year 2000? To solve this problem, we have to identify the values. The initial value is $12,000, which is the a-value. The rate is 1.5% or 0.015 as a decimal value. Also, 20 years passed from 1980 to 2000, which is time. Now we need to throw these values into the formula. We will use a minus sign in the formula because the car is depreciating in value.
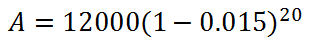
Cleaning up the parentheses we get...
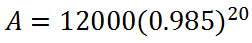
Throwing this into a calculator, we get this final value.
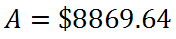
The Corvette lost more than $3,000.
| |
Here is a problem that deals with a precious stone.
If a $2000 diamond appreciates at a 3.9% annual rate, how much will it be worth 15 years from now?We need to identify the numbers in the problem. The $2000 is the starting amount (a-value). The 3.9%, or 0.039, is the rate (r-value). The 15 is time (t-value). Again, here is the formula.
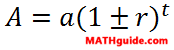
Now, we need to plug these numbers into the formula. We need to use a plus sign in the parentheses because the problem says 'appreciates.'
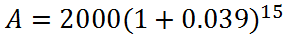
Simplifying the parentheses, we get this.
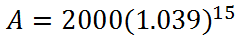
Using a calculator, we get this final amount.
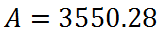
The diamond increased over $1500.
| |
Try this instructional video.
| |
Try this interactive quizmaster. | |
Try this lesson, which is related to the sections above.
| |
 ideo:
ideo:  uiz:
uiz:  esson:
esson: