Calculating Value Over Time 2 | ||
| ||
Introduction | ||
This lesson will inform you how to determine how long it will take for an item to change from one value to another value under an exponential growth or decay model. Here are the sections within this lesson page:
|
In our lesson called Calculating Value Over Time, we covered how the value of an item can change using an exponential growth/decay model. That lesson thoroughly explains how the function works. Likewise, we have a lesson on Logarithms that covers the various properties of exponents and logarithms.
It is strongly suggested that you review these lessons to ensure that the following sections can be properly understood.
| |
The formula that is used to calculate value over time is this.
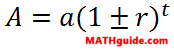
The variables are explained, as follows. The a-value represents the initial value of the item. The r-value is the rate. The t-value is time that elapses as the item changes from its initial value to its final value. Finally, the A-value is the final value of the item.
The sections that follow will explain how the formula is used to calculate for time as the value of an item changes from its starting amount to its final amount.
| |
Here is a problem that involves a sports car. A certain $30,000 sports car is said to depreciate in value at a 5.1% annual rate. How long will it take for the car to drop to $20,000?First, we need to place the values into the formula. To do this, we have to identify the known information. The a-value is $30,000. The A-value is $20,000. The r-value has to be determined by its percent, 5.1%. 5.1% is 5.1/100 or 0.051.
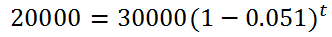
Notice that a subtraction sign was used because the car is going down in value. Continuing on, we can clean up the parentheses.
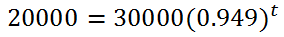
We have to get the base alone, which means we divide both sides of the equation by 30000 to get...
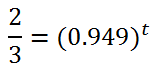
Next, convert this to log-form.
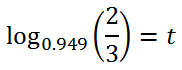
Using a calculator, we get our t-value, which is approximately 7.7 years. That sports car is going to drop a third of its value in slightly more than seven in a half years.
| |
Here is a problem that deals with a precious stone.
A $300 sapphire is estimated to appreciate in value at a 2.9% annual rate. How long will it take for the stone to double its value?Let us break down the numbers. The a-value is 300. The r-value is obtained by 2.9%, which is 2.9/100 or 0.029. Double its current value would be $600 and that is the A-value. This is what it looks like after we plug the numbers into the formula. We will use a plus sign because the stone is increasing its value over time.
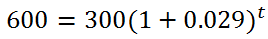
Cleaning up the parentheses, we get...
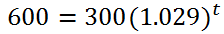
Next, we have to get the base alone, which means we have to divide both sides by 300. This is the result.
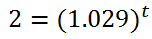
Now we have to convert this exponential equation into a logarithmic equation, like so.
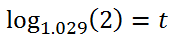
A calculator can now generate the solution, which is approximately 24.2 years.
| |
Watch this instructional video. | |
Try this interactive quizmaster. | |
Try this lesson, which is related to the sections above.
| |
 ideo:
ideo:  uiz:
uiz:  esson:
esson: