Dilations | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn about dilations. Here are the topics within this page:
|
Similar Figures -- a topic covered in another section -- can be described by the mathematics of dilations. Dilations have these features:
| |
When we refer to the original figure, of say a triangle, we call the original figure △ABC. We call the image figure △A'B'C'. The second triangle is pronounced, "triangle A-prime, B-prime, C-prime." | |
A characteristic called scale factor informs us of the relationship between the original figure and its image. The scale factor is typically called the k-value. When the k-value is 0 < k < 1 [greater than zero but less than one], the image figure is smaller than the original figure. When the k-value is k > 1 [greater than one], the image figure is greater than the original figure. This information is encapsulated within the diagram that follows.
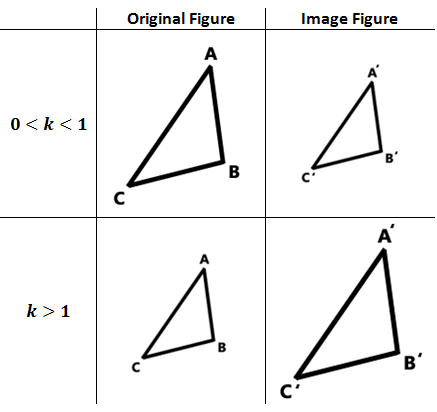
| |
Here is a quiz that can be used to test your understanding of dilations.
| |
This is a lesson that uses scale factors. After this lesson, students will be ready to move on to Areas and Lengths of Similar Figures and Volumes and Lengths of Similar Solids (see the related lessons section below).
| |
View these related lessons.
| |
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: