Arithmetic Sequences and Series | ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
Introduction | ||||||||||||||||||||||||||||
This page will teach you about arithmetic sequences and series. Here are the sections within this page:
| ||||||||||||||||||||||||||||
|
Sequences of numbers that follow a pattern of adding a fixed number from one term to the next are called arithmetic sequences. The following sequences are arithmetic sequences: Sequence A: 5 , 8 , 11 , 14 , 17 , ... For sequence A, if we add 3 to the first number we will get the second number. This works for any pair of consecutive numbers. The second number plus 3 is the third number: 8 + 3 = 11, and so on.
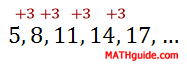 For sequence B, if we add 5 to the first number we will get the second number. This also works for any pair of consecutive numbers. The third number plus 5 is the fourth number: 36 + 5 = 41, which will work throughout the entire sequence. Sequence C is a little different because we need to add -2 to the first number to get the second number. This too works for any pair of consecutive numbers. The fourth number plus -2 is the fifth number: 14 + (-2) = 12. Because these sequences behave according to this simple rule of addiing a constant number to one term to get to another, they are called arithmetic sequences. So that we can examine these sequences to greater depth, we must know that the fixed numbers that bind each sequence together are called the common differences. Mathematicians use the letter d when referring to these difference for this type of sequence. Mathematicians also refer to generic sequences using the letter a along with subscripts that correspond to the term numbers as follows:
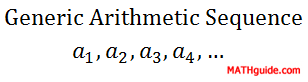 This means that if we refer to the fifth term of a certain sequence, we will label it a5. a17 is the 17th term. This notation is necessary for calculating nth terms, or an, of sequences. The d-value can be calculated by subtracting any two consecutive terms in an arithmetic sequence.
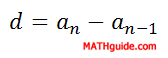
...where n is any positive integer greater than 1. Remember, the letter d is used because this number is called the common difference. When we subtract any two adjacent numbers, the right number minus the left number should be the same for any two pairs of numbers in an arithmetic sequence.
| ||||||||||||||||||||||||||||
To determine any number within an arithmetic sequence, there are two formulas that can be utilized. Here is the recursive rule.
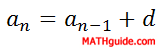 The recursive rule means to find any number in the sequence, we must add the common difference to the previous number in this list. Let us say we were given this arithmetic sequence.
First, we would identify the common difference. We can see the common difference is 4 no matter which adjacent numbers we choose from the sequence. To find the next number after 19 we have to add 4. 19 + 4 = 23. So, 23 is the 6th number in the sequence. 23 + 4 = 27; so, 27 is the 7th number in the sequence, and so on... What if we have to find the 724th term? This method would force us to find all the 723 terms that come before it before we could find it. That would take too long. So, there is a better formula. It is called the explicit rule.
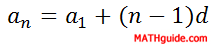 So, if we want to find the 724th term, we can use this explicit rule. Our n-value is 724 because that is the term number we want to find. The d-value is 4 because it is the common difference. Also, the first term, a1, is 3.
The rule gives us a724 = 3 + (724 - 1)(4) = 3 + (723)(4) = 3 + 2892 = 2895.
| ||||||||||||||||||||||||||||
Each arithmetic sequence has its own unique formula. The formula can be used to find any term we with to find, which makes it a valuable formula. To find these formulas, we will use the explicit rule. Let us also look at the following examples. Example 1: Let's examine sequence A so that we can find a formula to express its nth term. If we match each term with it's corresponding term number, we get:
The fixed number, called the common difference or d-value, is 3. We can substitute this information into the explicit rule an = a1 + (n - 1)d, like so. an = 5 + (n - 1)(3) an = 5 + 3n - 3 an = 3n + 2 a37 = 3(37) + 2 a37 = 111 + 2 a37 = 113 Here is sequence B.
We can identify a few facts about it. Its first term, a1, is 26. Its common difference or d-value is 5. We can substitute this information into the explicit rule.
an = 26 + (n - 1)(5) an = 26 + 5n - 5 an = 5n + 21
a14 = 5(14) + 21 a14 = 70 + 21 a14 = 91  ideo: Finding the nth Term of an Arithmetic Sequence ideo: Finding the nth Term of an Arithmetic Sequence uizmaster: Finding Formula for General Term uizmaster: Finding Formula for General Term
| ||||||||||||||||||||||||||||
It may be necessary to calculate the number of terms in a certain arithmetic sequence. To do so, we would need to know two things. We would need to know a few terms so that we could calculate the common difference and ultimately the formula for the general term. We would also need to know the last number in the sequence. Once we know the formula for the general term of a sequence and the last term, the procedure involves the use of algebra. Use the two examples below to see how it is done. Example 1: Find the number of terms in the sequence 5, 8, 11, 14, 17, ..., 47. This is sequence A. In the previous section, we found the formula to be an = 3n + 2 for this sequence. We will use this along with the fact the last number, an, is 47. We will plug this into the formula, like so... 47 = 3n + 2 45 = 3n 15 = n n = 15 Example 2: Find the number of terms in the arithmetic sequence 20, 18, 16, 14, 12, ...,-26. Our first task is to find the formula for this sequence given a1 = 20 and d = -2. We will substitute this information into the explicit rule, like so. an = 20 + (n - 1)(-2) an = 20 - 2n + 2 an = -2n + 22 -26 = -2n + 22 -48 = -2n 24 = n n = 24
| ||||||||||||||||||||||||||||
Given our generic arithmetic sequence...
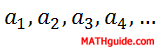 ...we can add the terms, called a series, as follows.
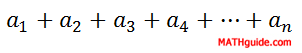 There exists a formula that can add such a finite list of these numbers. It requires three pieces of information. The formula is...
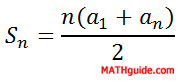 ...where Sn is the sum of the first n numbers, a1 is the first number in the sequence and an is the nth number in the sequence. If you would like to see a derivation of this arithmetic series sum formula, watch this video.
Usually problems present themselves in either of two ways. Either the first number and the last number of the sequence are known or the first number in the sequence and the number of terms are known. The following two problems will explain how to find a sum of a finite series. Example 1: Find the sum of the series 5 + 8 + 11 + 14 + 17 + ... + 128. In order to use the sum formula. We need to know a few things. We need to know n, the number of terms in the series. We need to know a1, the first number, and an, the last number in the series. We do not know what the n-value is. This is where we must start.
To find the n-value, let's use the formula for the series. We already determined the formula for the sequence in a previous section. We found it to be an = 3n + 2 128 = 3n + 2 126 = 3n 42 = n n = 42 S42 = (1/2)(42)(5 + 128) S42 = (21)(133) S42 = 2793 Example 2: Find the sum of the first 205 multiples of 7. First we have to figure out what our series looks like. We need to write multiples of seven and add them together, like this. To find the last number in the series, which we need for the sum formula, we have to develop a formula for the series. So, we will use the explicit rule or an = a1 + (n - 1)d. We can also see that d = 7 and the first number, a1, is 7. an = 7 + (n - 1)(7) an = 7 + 7n - 7 an = 7n an = 7(205) an = 1435 To find the sum, we will substitute information into the sum formula. We will substitute a1 = 7, a205 = 1435, and n = 205. S42 = (1/2)(205)(7 + 1435) S42 = (1/2)(205)(1442) S42 = (1/2)(1442)(205) S42 = (721)(205) S42 = 147805
|
Watch these instructional videos.
|
After reading the lesson, try our quizmaster. MATHguide has developed numerous testing and checking programs to solidify skills demonstrated in this lesson. The following quizmasters are available:
|
After reading the lesson, try a related lesson or quizmaster.
|
 esson:
esson: